0

I guess that ABCD matrices are not intended for one port, but, in this case, for the purpose of cascading two networks, 2 port (impedance transformer) and 1 port (antenna), by ABCD matrix multiplication, I want to represent antenna impedances - as ABCD matrix.

I found this form, but I'm not sure, if it is correct:

$$ \Biggl[ \begin{matrix} 1 & Z(f)\\ 0 & 1\\ \end{matrix} \Biggl] $$

Julien
  • 1,717
  • 14
Danko Dnevic
  • 45
  • 6

3 Answers3

1

I know that is not usual to answer own questions, but I found solution (searching through web + experimenting with parameters) and for the sake of other members, who might have same ambiguity, here is the answer. 1 port impedance termination, is representable as ABCD matrix as admittance shunt. Therefore solution is:

$$ \Biggl[ \begin{matrix} 1 & 0\\ 1/Z(f) & 1\\ \end{matrix} \Biggl] $$

Where Z(f) is (complex) impedance for given frequency. I have tested above form, by multiplication 2 port ABCD matrix with ABCD matrix forged this way (as cascaded termination). It works just fine.

Danko Dnevic
  • 45
  • 6
1

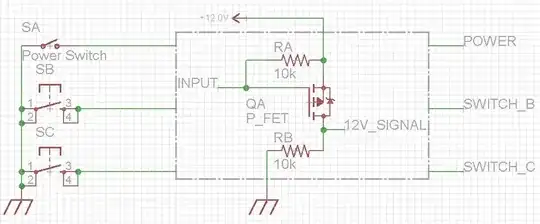
schematic

simulate this circuit – Schematic created using CircuitLab

The port impedance of an ABCD matrix, with an impedance applied to the opposite port, is easily derived from the definition: $$ \begin{eqnarray} V_1 = &\, A V_2 + B I_2 \\ I_1 = &\, C V_2 + D I_2 \end{eqnarray} $$

From the definition, we see that a "standalone impedance" is meaningless, because an ABCD matrix is strictly relational (port 1 in terms of port 2, or vice versa by its inverse). We can have an impedance (or conductance) if we stipulate that port 2 must be open-circuit (V2 = V1, I2 = 0; A = 1, B = 0, C = Y, D = 0), or short-circuit (V2 = 0, I2 = I1; A = 0, B = Z, C = 0, D = 1)[1], but we can preferably use the matrix as it was designed to do, and apply the impedance directly.

Applying an impedance to port 2, we have:

$$ \begin{eqnarray} V_2 = &\, I_2 Z_2 \\ Z_1 = &\, \dfrac{V_1}{I_1} \end{eqnarray} $$

Thus we obtain,

$$Z_1 = \frac{A Z_2 + B}{C Z_2 + D}$$

Further reading: A Review of ABCD Parameters

[1] I suppose the zero parameters (B and D, or A and C) are really undefined, given the assumption that the respective port 2 value is zero. But I would rather not have to remember assumptions, and just work with it properly.

Tim Williams
  • 22,874
  • 1
  • 20
  • 71
  • This is correct, but how to preserve ABCD matrix modularity, in this case? If we need more then just input impedance, i.e. cascaded matrix, which we can use later? – Danko Dnevic Aug 11 '23 at 21:16
  • 1
    Multiply the ABCDs in the system beforehand. Or use the same formula and apply this impedance to the next matrix and so on. (Ab)using an ABCD for the same purpose leaves the ambiguity of order of multiplication, for which multiplying the antenna/match network on the right-hand side would be rather problematic (i.e., putting a network "after" the antenna). – Tim Williams Aug 11 '23 at 22:14
  • Parallel antennas? :-) – Danko Dnevic Aug 11 '23 at 22:19
  • More like, putting a box (of unspecified material) around the antenna as a balun or matching or filtering or whatever. Which... I mean, given the right materials and geometry, you might be able to affect such a thing. But doing it in free fields is exponentially more difficult than doing it in the transmission line. And it almost certainly won't have the same parameters as that simple little balun you had hoped to wire inline to it. :-) – Tim Williams Aug 11 '23 at 23:14
0

The ABCD matrix is indeed only for 2-port devices. I think the parameters you should use are the S-parameters. Your antenna will be represented as an S1P device (so a 1×1 matrix with only its complex impedance). Then your matching circuit will be represented by a 2-port device (S2p) (2×2 matrix). To cascade them, S-parameters aren't convenient. So you should convert them in T-parameters. These can be cascaded easily then brought back to S-parameters.

That can be a lot of calculation. Lucky you, since you are cascading a simple impedance, you are not obligated to pass trough the T-parameters. You can simply find the S matrix of your matching network then add a termination to it. You can do your calculation of S11 and you should find the impedance at the input of your matching network, which is also the S1P matrix of your system.

Another way to solve that system is using Mason's rule. For such simple circuit, it shouldn't be hard. You might even find it as an example in many books!

If you aren't familiar on S-parameters, you can find many sources that would explain them much better then me!

Tim Williams
  • 22,874
  • 1
  • 20
  • 71
Julien
  • 1,717
  • 14
  • Same question for one port T parameters. How to get T matrix, from Zload (or S11) only? – Danko Dnevic Aug 09 '23 at 22:06
  • Well, I never done it via T matrix because it is simpler to just calculate it from the S parameters. But logically, the 2 port S device will generate a square 2*2 T matrix. Your 1 port device would be a 2 by 1. But, that would give you one to many degree of freedom. So, your termination should be a 3*1 matrix and the 2 port should then be a 3*2 matrix. To be fair, reducing or increasing port number always confused me with T matrix, but there is a great book on the matter. Janusz Dobrowolski: Introduction to computer methods for microwave circuit analysis and design – Julien Aug 09 '23 at 22:20