Reduction for Analysis
I've reduced the first stage of your schematic to a more behavioral one for analysis:
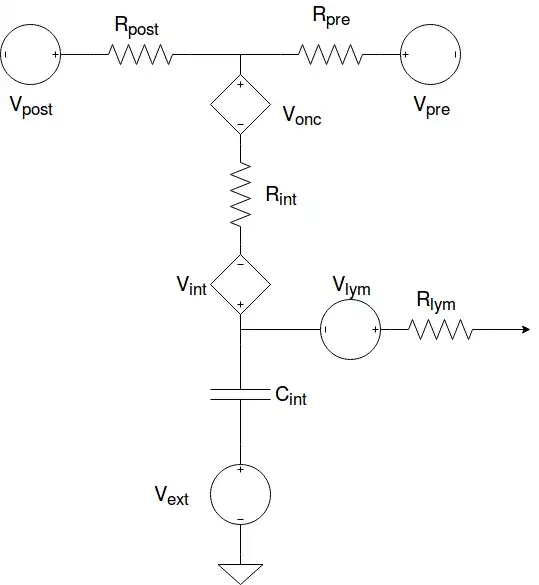
simulate this circuit – Schematic created using CircuitLab
From the above, we know:
$$\begin{align*}
V_{_\text{O}}\cdot\frac{1+\frac{R_2}{R_3}}{1+\frac{R_6}{R_7}}&=\frac{\frac{V_{_\text{O}}}{1+\frac{R_4}{R_5}}\,\cdot\,R_1+V_{_\text{I}}\,\cdot\,R_{_\text{TH}}}{R_1+R_{_\text{TH}}+\frac{R_1\,\cdot\,R_{_\text{TH}}}{R_2+R_3}}
\end{align*}$$
Loop Gain and Closed Loop Gain
From that, find:
$$\begin{align*}
V_{_\text{O}}\cdot\left(1-\frac{\frac{1}{1+\frac{R_4}{R_5}}\,\cdot\,R_1}{R_1+R_{_\text{TH}}+\frac{R_1\,\cdot\,R_{_\text{TH}}}{R_2+R_3}}\cdot\frac{1+\frac{R_6}{R_7}}{1+\frac{R_2}{R_3}}\right)&=V_{_\text{I}}\,\cdot\,\frac{R_{_\text{TH}}}{R_1+R_{_\text{TH}}+\frac{R_1\,\cdot\,R_{_\text{TH}}}{R_2+R_3}}\cdot\frac{1+\frac{R_6}{R_7}}{1+\frac{R_2}{R_3}}
\end{align*}$$
That's in the form of \$V_{_\text{O}}\cdot\left(1-B\cdot A\right)=V_{_\text{I}}\cdot A\$ with \$A=\frac{R_{_\text{TH}}}{R_1+R_{_\text{TH}}+\frac{R_1\,\cdot\,R_{_\text{TH}}}{R_2+R_3}}\cdot\frac{1+\frac{R_6}{R_7}}{1+\frac{R_2}{R_3}}\approx 0.877\$ and therefore \$B=\frac{R_1}{R_{_\text{TH}}}\cdot \frac{1}{1+\frac{R_4}{R_5}}\approx 0.419\$.
It's also in the positive/regenerative feedback form, as you already identified. So \$B\$ is positive feedback. The loop gain is \$A\cdot B\approx 0.368\$ and since this is less than 1 the system converges on the overall closed loop gain of \$\frac{V_{_\text{O}}}{V_{_\text{I}}}=\frac{A}{1-B\,\cdot\, A} \approx 1.39\$.
So, expanding \$\frac{A}{1-B\,\cdot\, A}\$, the final closed loop gain equation is:
$$A_v=\frac{1+\frac{R_6}{R_7}}{\frac{R_1}{R_3}+\left(1+\frac{R_2}{R_3}\right)\,\cdot\,\left(1+\frac{R_1}{R_4}+\frac{R_1}{R_5}\right)-\frac{R_1}{R_4}\,\cdot\,\left(1+\frac{R_6}{R_7}\right)}$$
Let's test both:
def par(a,b): return a*b/(a+b) # a and b taken in parallel
a = par(r4,r5)/(r1+par(r4,r5)+r1*par(r4,r5)/(r2+r3))*(1+r6/r7)/(1+r2/r3)
b = r1/par(r4,r5)/(1+r4/r5)
(a/(1-b*a)).subs( { r1:1.76e3, r2:3.64e3, r3:1.76e3, r4:4.2e3
, r5:1.87e3, r6:3.34e3, r7:536 } )
1.38762233798678 # computed using A/(1-B*A)
(r6/r7 + 1) / (r1/r3 + (r2/r3 + 1)*(1 + r1/r5 + r1/r4) - r1/r4*(r6/r7 + 1)).subs(
{ r1:1.76e3, r2:3.64e3, r3:1.76e3, r4:4.2e3
, r5:1.87e3, r6:3.34e3, r7:536 } )
1.38762233798678 # computed using expanded version
Note that they are both equivalent to each other. Just two different ways of saying the same thing. So the voltage gain is \$20\cdot\log_{10}\left(1.38762233798678\right)\approx 2.84542565\:\text{dB}\$
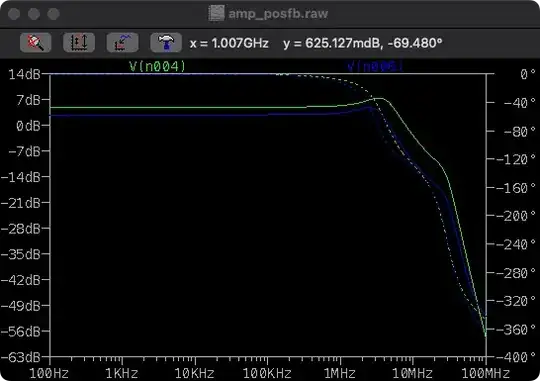
I've added a test using LTspice (performed a day after the answer was written):
Seems that LTspice agrees.
Input Impedance
To get this, I simply derived it by first taking the voltage difference across \$R_1\$ and dividing that by \$R_1\$ to get the current in \$R_1\$. This current was then divided into the input voltage in order to work out the impedance. It's straight-forward.
The input impedance thus seen by the source will be:
$$R_{_\text{I}}=R_1\cdot\frac{1}{1-\frac{V_{_\text{O}}}{V_{_\text{I}}}\cdot\frac{1+\frac{R_2}{R_3}}{1+\frac{R_6}{R_7}}}\approx 2.432\times R_1\approx 4.28\:\text{k}\Omega $$
Schematic Notes
The following shows my notations for the schematic used to derive the above: