0

In the Figure shows what is the function of 0 and determines its value when V0 = −3V1 − 2V2.

enter image description here

Circuit fantasist
  • 13,593
  • 1
  • 17
  • 48
NAMAN GARG
  • 1
  • NAMAN, With the help of these answers, you probably will be able to answer the question... but more important is if you understand the problem. Can you answer the following questions: What are these currents? Where do they flow? What produces them? What voltage drops do they create? How do they destroy each other? – Circuit fantasist Jul 29 '23 at 10:20

3 Answers3

1

I can think of two functions:

  • Bias current compensation by presenting the same impedance to the positive and to the negative input of the op amp (unnecessary for most modern amplifier architectures).
  • Current limitation: If a voltage bigger than the amplifier's supply voltage is present at an input, internal (ESD-)protection diodes might become conductive and eventually destroyed, if the current isn't limited. However, in an inverting configuration an over-voltage condition at the non-inverting input is probably less likely than at the inverting input, where the signal is fed into (depends on the application, of course).

For bias current compensation the value of R0 depends on the source impedance of V1 and V2. Assuming zero source impedance for V1 and V2, R0 is simply the parallel combination of R1, R2 and 6K. So inverting and non-inverting input "see" the same impedance to the reference voltage.

For current limiting R0 should limit the current to a safe value, i. e. a value smaller than the "absolute maximum" input current specified in the datasheet.

feynman
  • 2,466
  • 3
  • 10
0

what is the function of 0

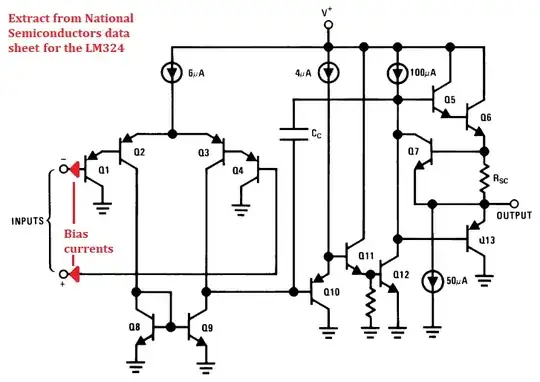
\$R_0\$ reduces the output voltage DC error due to bias currents produced by the op-amp inputs.

For example, an LM324 op-amp has an input bias current of about 40 nA (supplier dependant). This will cause a 40 mV input offset voltage error when the net resistance value at the inverting input is 1 MΩ. If you have a gain of (say) ten, the output voltage error will be 400 mV.

If you use a 1 MΩ resistor for \$R_0\$, this error is minimized due to similarity of input bias currents.

enter image description here

determine its value when V0 = −3V1 − 2V2

Well, if you can calculate \$R_1\$ and \$R_2\$, \$R_0\$ is equal to \$R_1\$ || \$R_2\$ || 6k.

It's got nothing to do with input pin protection in your mixer circuit.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
0

A Hint: Use nodal analysis to solve for Vo. Recall that nodal voltages at + and - terminals of the Op-amp are same so you can combine + amd - nodes as a same node V. The reason for using R0 seems to be given by other authors.

Amit M
  • 394
  • 1
  • 11