Current passing through voltage source using nodal analysis

Question

I did a nodal analysis on this circuit where I put the reference node at the middle part.

The question was to find the current passing through 10V source using nodal analysis. I tried answering it like this in the picture but the answer key says it should be 3.55 A

I tried other equations to get the 3.55A and I got it by I1 - I3 = 3.5537A but I think its wrong. What is the error that I did?

But how can this be true? The current that passes through 10V source is equal to (10V - 7.107V)/5Ω = 578.6mA. And how can it be otherwise? — G36, Jul 20 '23 at 16:34
@G36 that’s what I’ve been trying to find because the current that I always got is 578.6mA. The answer key in the book was 3.55A but I still don’t get it — mama b, Jul 20 '23 at 16:39
The book's answer is wrong, nothing new here. The 2 Ohms resistor is equal to 7.107V/2Ω = 3.5535A. — G36, Jul 20 '23 at 16:42
Rounding a number (My calculator displayed 3.553719008, by the way) to three significant digits doesn't necessarily make it "wrong." Although, if the book answer was rounded to three digits, it would have been polite for the author to tell you so. — Solomon Slow, Jul 20 '23 at 17:02
@SolomonSlow yes, but the answer 3.55 was supposedly for the 2 ohm resistor. Maybe the book was wrong here. — mama b, Jul 20 '23 at 17:13

score 0 · Accepted Answer · answered Jul 23 '23 at 14:48

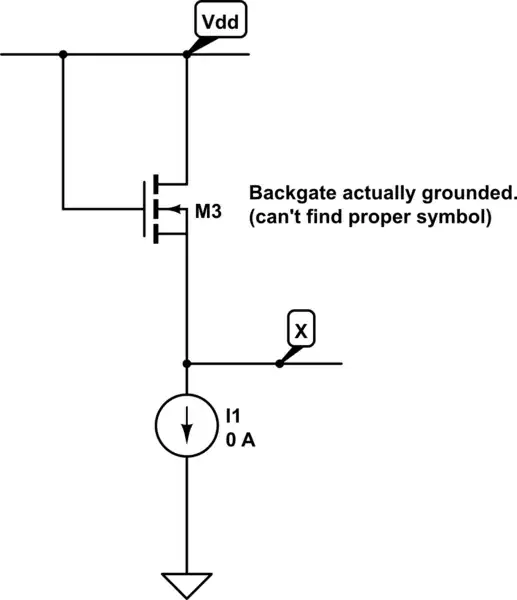
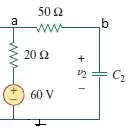
Well, we are trying to analyze the following circuit:

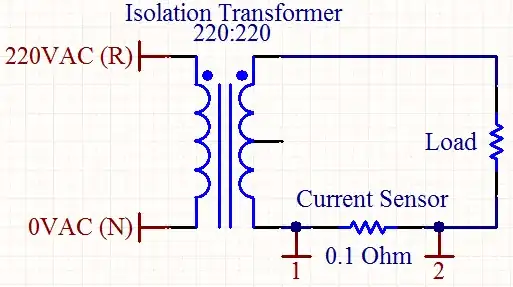
schematic

^{simulate this circuit – Schematic created using CircuitLab}

When we use and apply KCL, we can write the following set of equations:

$$ \begin{cases} \begin{alignat*}{1} \text{I}_2&=\text{I}_1+\text{I}_4\\ \\ 0&=\text{I}_0+\text{I}_1+\text{I}_5\\ \\ 0&=\text{I}_0+\text{I}_2+\text{I}_3\\ \\ \text{I}_5&=\text{I}_3+\text{I}_4 \end{alignat*} \end{cases}\tag1 $$

When we use and apply Ohm's law, we can write the following set of equations:

$$ \begin{cases} \begin{alignat*}{1} \text{I}_1&=\frac{\displaystyle\text{V}_\text{a}-\text{V}_1}{\displaystyle\text{R}_1}\\ \\ \text{I}_2&=\frac{\displaystyle\text{V}_1-0}{\displaystyle\text{R}_2}\\ \\ \text{I}_3&=\frac{\displaystyle\text{V}_3-0}{\displaystyle\text{R}_3}\\ \\ \text{I}_4&=\frac{\displaystyle\text{V}_2-\text{V}_1}{\displaystyle\text{R}_4}\\ \\ \text{I}_5&=\frac{\displaystyle0-\text{V}_3}{\displaystyle\text{R}_5} \end{alignat*} \end{cases}\tag2 $$

We also know that \$\displaystyle\text{V}_2-\text{V}_3=\text{V}_\text{b}\$.

Using \$(2)\$ we can rewrite \$(1)\$ as follows:

$$ \begin{cases} \begin{alignat*}{1} \frac{\displaystyle\text{V}_1-0}{\displaystyle\text{R}_2}&=\frac{\displaystyle\text{V}_\text{a}-\text{V}_1}{\displaystyle\text{R}_1}+\frac{\displaystyle\text{V}_2-\text{V}_1}{\displaystyle\text{R}_4}\\ \\ 0&=\text{I}_0+\frac{\displaystyle\text{V}_\text{a}-\text{V}_1}{\displaystyle\text{R}_1}+\frac{\displaystyle0-\text{V}_3}{\displaystyle\text{R}_5}\\ \\ 0&=\text{I}_0+\frac{\displaystyle\text{V}_1-0}{\displaystyle\text{R}_2}+\frac{\displaystyle\text{V}_3-0}{\displaystyle\text{R}_3}\\ \\ \frac{\displaystyle0-\text{V}_3}{\displaystyle\text{R}_5}&=\frac{\displaystyle\text{V}_3-0}{\displaystyle\text{R}_3}+\frac{\displaystyle\text{V}_2-\text{V}_1}{\displaystyle\text{R}_4} \end{alignat*} \end{cases}\tag3 $$

Solving this for your circuit we get:

In[1]:=Clear["Global`*"];
Va = 10;
Vb = 20;
R1 = 5;
R2 = 2;
R3 = 4;
R4 = 3;
R5 = 2;
FullSimplify[
 Solve[{I2 == I1 + I4, 0 == I0 + I1 + I5, 0 == I0 + I2 + I3, 
   I5 == I3 + I4, I1 == (Va - V1)/R1, I2 == (V1 - 0)/R2, 
   I3 == (V3 - 0)/R3, I4 == (V2 - V1)/R4, I5 == (0 - V3)/R5, 
   V2 - V3 == Vb}, {I0, I1, I2, I3, I4, I5, V1, V2, V3}]]

Out[1]={{I0 -> -(310/121), I1 -> 70/121, I2 -> 430/121, I3 -> -(120/121), 
  I4 -> 360/121, I5 -> 240/121, V1 -> 860/121, V2 -> 1940/121, 
  V3 -> -(480/121)}}

In[2]:=N[%]

Out[2]={{I0 -> -2.56198, I1 -> 0.578512, I2 -> 3.55372, I3 -> -0.991736, 
  I4 -> 2.97521, I5 -> 1.98347, V1 -> 7.10744, V2 -> 16.0331, 
  V3 -> -3.96694}}

Current passing through voltage source using nodal analysis

1 Answers1