RC time constant: theoretical vs LTSpice

Question

I was preparing this lab sheet and the circuit we are analyzing is

The theoretical time constant of this circuit is given by

$$\tau=R_{th}C_1=\left(R_1 // R_2 + R_3\right)C_1 \simeq 207.3 \,\, \mu s $$

Nice and straightforward.

Now to analyze the circuit I have considered the ideal source, resistors and also forced the capacitor to be ideal.

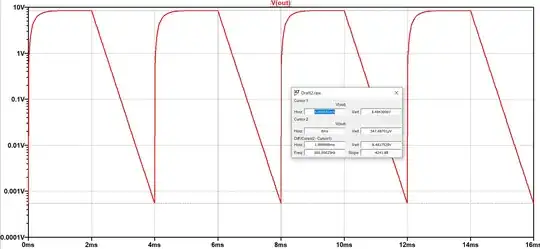
I have obtained this logarithmic plot of the output voltage

The thought process was considering the discharge of the capacitor

$$V_{out}= V_{charge} \times e^{-\frac{t}{\tau}}$$

with

$$V_{charge} = \frac{R_2}{R_1+R_2} \times V_{ON} \simeq 8.485 \,\, V $$

Taking the logarithm means that the time constant is given by the inverse of the slope

$$ \ln \left(V_{out} \right) = \ln \left(V_{charge} \right) - \frac{t}{\tau} $$

From the graph and the plot points follows that

$$\tau \approx 235.7 \,\, \mu s$$

So there is a difference of \$ 28.4 \,\, \mu s \$ between the theoretical and simulated value.

I am trying to find the reason behind this.

At first I was like "well there are some imprecisions on using the cursor values, due to the discretization so perhaps there is a change on the slope by considering this two points.

But then I did the "pseudo-theoretical" calculation of the time constant by considering that the capacitor discharges from \$ V_{charge} \$ to \$ 0 \$ during half the period \$ \left(2 \,\, m s \right) \$, which gives \$ \tau = \frac{2 \,\, m s}{V_{charge} - 0} \simeq 235.7 \,\, \mu s \$ so it is not due to imprecisions with the cursors the "pseudo-theoretical" calculation gives a similar value.

There might be something I am overseeing in this? Perhaps the slope method is also an approximation somehow to the time constant? What is exactly going on here?

Answer 1

Looking at the cursors on your plot, I can see the bottom of the discharge section is given by \$547.69701\mu V\$.

Plugging this into your own equation:

$$\tau = \frac{2ms}{\ln\left(\frac{10V}{547.69701\mu V}\right)} = 203.824285\mu s$$

That is far from the \$28.4\mu s\$ difference you got (\$3.473\mu s\$). In order to be fully perfect, we can also account for the different DC voltage.

$$V_{max} = 10V\cdot \frac{56k\Omega}{56k\Omega + 10k\Omega} \approx 8.485V$$

The new time constant becomes

$$\tau = \frac{2ms}{\ln\left(\frac{8.485V}{547.69701\mu V}\right)}\approx 207.295$$

You can see where this is going. You can also start accounting for the limited rise/fall time of the source for example to get even closer.

If you're still not satisfied, small differences can often be attributed to truncation errors of the transient analysis or numerical errors in either computation or integration.

Answer 2

ln(547E-6) - ln(8.483) = -9.649

Which gives us \$\tau \approx\$ 207.3us

Answer 3

Well, notice that by using the convolution theorem of the Laplace transform, we know that the output waveform is given by:

\begin{equation} \begin{split} \text{V}_\text{o}\left(t\right)&=\mathscr{L}_\text{s}^{-1}\left[\frac{\displaystyle1}{\displaystyle\text{sC}}\cdot\text{v}_\text{i}\left(\text{s}\right)\cdot\left(\text{R}_1+\frac{\displaystyle\text{R}_2\cdot\left(\text{R}_3+\frac{1}{\text{sC}}\right)}{\displaystyle\text{R}_2+\text{R}_3+\frac{1}{\text{sC}}}\right)^{-1}\right]_{\left(t\right)}\\ \\ &=\frac{1}{\text{C}}\int\limits_0^t\mathscr{L}_\text{s}^{-1}\left[\text{v}_\text{i}\left(\text{s}\right)\cdot\left(\text{R}_1+\frac{\displaystyle\text{R}_2\cdot\left(\text{R}_3+\frac{1}{\text{sC}}\right)}{\displaystyle\text{R}_2+\text{R}_3+\frac{1}{\text{sC}}}\right)^{-1}\right]_{\left(\tau\right)}\space\text{d}\tau\\ \\ &=\frac{1}{\text{C}}\int\limits_0^t\int\limits_0^\tau\mathscr{L}_\text{s}^{-1}\left[\text{v}_\text{i}\left(\text{s}\right)\right]_{\left(\sigma\right)}\cdot\mathscr{L}_\text{s}^{-1}\left[\left(\text{R}_1+\frac{\displaystyle\text{R}_2\cdot\left(\text{R}_3+\frac{1}{\text{sC}}\right)}{\displaystyle\text{R}_2+\text{R}_3+\frac{1}{\text{sC}}}\right)^{-1}\right]_{\left(\tau-\sigma\right)}\space\text{d}\sigma\space\text{d}\tau\\ \\ &=\frac{1}{\text{C}}\int\limits_0^t\int\limits_0^\tau\text{V}_\text{i}\left(\sigma\right)\cdot\mathscr{L}_\text{s}^{-1}\left[\left(\text{R}_1+\frac{\displaystyle\text{R}_2\cdot\left(\text{R}_3+\frac{1}{\text{sC}}\right)}{\displaystyle\text{R}_2+\text{R}_3+\frac{1}{\text{sC}}}\right)^{-1}\right]_{\left(\tau-\sigma\right)}\space\text{d}\sigma\space\text{d}\tau\\ \\ &=\frac{1}{\text{C}}\int\limits_0^t\int\limits_0^\tau\text{V}_\text{i}\left(\sigma\right)\cdot\mathscr{L}_\text{s}^{-1}\left[\left(\text{R}_1+\frac{\displaystyle\text{R}_2\left(\text{sCR}_3+1\right)}{\displaystyle\text{sC}\left(\text{R}_2+\text{R}_3\right)+1}\right)^{-1}\right]_{\left(\tau-\sigma\right)}\space\text{d}\sigma\space\text{d}\tau\\ \\ &=\frac{1}{\text{C}}\int\limits_0^t\int\limits_0^\tau\text{V}_\text{i}\left(\sigma\right)\cdot\mathscr{L}_\text{s}^{-1}\left[\frac{\displaystyle\text{sC}\left(\text{R}_2+\text{R}_3\right)+1}{\displaystyle\text{R}_1\left(\text{sC}\left(\text{R}_2+\text{R}_3\right)+1\right)+\text{R}_2\left(\text{sCR}_3+1\right)}\right]_{\left(\tau-\sigma\right)}\space\text{d}\sigma\space\text{d}\tau\\ \\ \end{split}\tag1 \end{equation}