I am practicing nodal analysis using the book "Fundamentals of Electric Circuits," and I have encountered two problems in which I obtained negative answers, whereas the book provides positive solutions.
Example 1:
vs
Example 2:
vs
Can my work can still be considered correct?
+1 from me for showing your efforts. It's easily enough to earn a moments response.
You can check your own work. I'll just dash out mine for comparison. I disagree with you on 3.9 and agree with the authors. I agree with you on 3.10 and disagree with the authors.
The nodal looks like this to me:
$$\frac{v_1}{250\:\Omega}+\frac{v_1}{50\:\Omega}+\frac{v_1-60\cdot\frac{24\:\text{V}-v_1}{250\:\Omega}}{150\:\Omega}=\frac{24\:\text{V}}{250\:\Omega}+\frac{0\:\text{V}}{50\:\Omega}+\frac{0\:\text{V}}{150\:\Omega}$$
Using SymPy I get:
solve(Eq(vx1/50+vx1/250+(vx1-60*(24-vx1)/250)/150,24/250),vx1)[0].n()
4.16528925619835
The nodal looks like this to me:
$$\begin{align*} \frac{v_1}{8\:\Omega}+\frac{v_1}{1\:\Omega}+4\:\text{A}&=\frac{0\:\text{V}}{8\:\Omega}+\frac{v_3}{1\:\Omega} \\\\ \frac{v_2}{2\:\Omega}+2\cdot\frac{v_1}{8\:\Omega}&=4\:\text{A}+\frac{0\:\text{V}}{2\:\Omega} \\\\ \frac{v_3}{4\:\Omega}+\frac{v_3}{1\:\Omega}&=2\cdot\frac{v_1}{8\:\Omega}+\frac{0\:\text{V}}{4\:\Omega}+\frac{v_1}{1\:\Omega} \end{align*}$$
Using SymPy I get:
solve([Eq(vx1/8+vx1/1+4,vx3/1),
Eq(vx2/2+2*vx1/8,4),
Eq(vx3/4+vx3/1,2*vx1/8+vx1/1)],[vx1,vx2,vx3])
{vx1: -32, vx2: 24, vx3: -32}
Who are we but ignorants when compared to the authors?
Let LTspice resolve it for us:
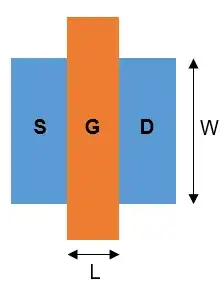
Adding a note about how you can also just check their answers, quickly. When you see something you disagree with, it's a good idea to just take their answers as granted and then apply them to the schematic. If you find a logical conflict -- some unknown that must have two simultaneously different values for example -- then you know they made a mistake.
Doing that I find (putting the order of steps I took on the sheet as well):
Their answer has been cornered.
The above is something you didn't do but I know you could have done it quickly on your own. You know this stuff well enough to rapidly lay these details out and it may alter how you frame questions, too.
Assuming that you have their results in some fashion ahead of time, then get in the practice of just jumping forward to do this kind of fast sanity check. Doing it first before anything else can save you some serious time.
You already have a beautiful answer, so I will just add the parts that went wrong:
3.9: You got \$I_b\$ wrong, it should be \$\frac{24V-v_1}{250\:\Omega}\$ not \$\frac{-24V-v_1}{250\:\Omega}\$.
But since you stay consistent in entering all your voltages as negative of what they should be, your (correct) solve of the (incorrect) equation gives you a result that is correct except for the sign.
3.10: The book lists the correct equations, however it has an error in the simplification/reduction stage. The equation at node 1: \$\frac{v_1-0}{8} + \frac{v_1-v_3}{1} + 4 = 0\$
Reduces to: \$1.125\:v_1 - v_3 + 4 = 0\$, but they list it as \$1.125\:v_1 - v_3 = 4\$, and this leaves them with a sign error that carries through to the result.
