2

schematic

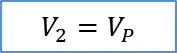
simulate this circuit – Schematic created using CircuitLab

Naming the top two loop currents clockwise as i1 and i2 and the bottom two as i3 and i4. By inspection, we can say $$i_1=-1A$$ Now, loop equation on mesh 2 gives,

$$-8-1(i_2-i_4)-1(i_1-i2)=0$$ Upon solving, we get, $$i_4=7A$$

whereas by using Nodal Analysis, $$\frac{V_1-0}{1}+\frac{V_1-8}{1}+\frac{V_1-0}{1}+\frac{V_1-8}{1}=0$$ Solving, we get, $$4V_1-16=0\Rightarrow V_1=4V$$

Applying KCL, we get $$i+\frac{(0-V_1)}{1}+5=0$$

Therefore, $$i=-1A$$

I am getting the answer as -1A (which is the correct answer). What am I doing wrong in the Mesh Analysis part?

Bruce Wayne
  • 87
  • 5
  • 1
    It looks like your loop equation on mesh 2 is wrong on the sign for one of the \$i_2\$ quantities and, I don't think they cancel out. – Andy aka Jun 27 '23 at 08:43
  • 2
    Looks like you already have your answer. But Just wanted to say how refreshing it is to see someone showing their attempts to learn where they went wrong rather than expecting others to do it all for them! – MCG Jun 27 '23 at 09:00
  • @Andyaka Got it. Thanks. I think its better to name the currents first and then solve rather than getting it wrong. – Bruce Wayne Jun 27 '23 at 09:48
  • @MCG I couldn't agree more. – Bruce Wayne Jun 27 '23 at 09:50

1 Answers1

2

The loop equation on mesh 2 is wrong - more specifically, by your definition of the direction of \$i_1\$ and \$i_2\$, the voltage drop on \$R_1\$ that is "contributing" to the loop voltage should be calculated as such:

$$V_{R_1} = (i_1-i_2) \cdot R_1 = +1(i_1-i_2)$$

VR1

So the KVL on mesh 2 would be: $$-8 -1(i_2-i_4) +1(i_1-i_2) = 0$$

uriyabsc
  • 493
  • 3
  • 13