Transistor functionality confusion

Question

Overview

I'm reading a book about the basics of electronics and I've gotten to the section on transistors and it's brought up some confusion for me. I first understood Transistors to be basically electronic switches in which the collector and emitter would become "connected" once a voltage was applied to the base. In the book, transistors are described as current controllers. Then the Beta value is the coefficient of the base current. So for example, if you applied 1mA of current to the base of a transistor with a Beta value of 5 then a max of 5mA would be allowed to flow.

---

Questions

So my main questions are these:

1: Switching Power

• The book says that for NPN transistors the base voltage (I'm assuming between base and GND) has to be larger than the voltage at the emitter (again,I think between GND.) How exactly would this work?

• First how would a transistor stay in the on-state if once you applied voltage to the base the emitter got powered then wouldn't that cause the emitter to have a higher voltage than the base thus shut it off?
• Second how does this work like in physics? What's causing that current draw at the base if it's not connected to GND?

2: Amplification

• If the Beta value is the value by which the current is multiplied at the base then is that just maximum current? Going back to the example of 1mA at base with Beta value of 5, is the 5mA just the maximum allowed current to flow between the collector and the emitter or does it like amplify the current? I'm a bit confused.

3: Variance

• How do PNP transistors fit into all of this?

Answer 1

You probably need to review potential, and what it means. As a reminder:

• Voltage across something (for instance a base-emitter junction) is the difference between potentials at two different points in a circuit (base and emitter, for instance). Because this a difference, the voltage "across" or "between two points", is independent of any other potential anywhere else. The two nodes in question could have potentials +1000000V and +1000001V, or -0.5V and +0.5V, the difference is the same, 1V.

• Voltage at some point in a circuit is the potential difference between that point and some arbitrarily chosen "ground", or "zero volts" node.

This means that you have to be careful how you use phrase statements about voltage (potential). If you say "across" a thing or "between" two points, or perhaps "over" a thing, everybody knows what you mean - the difference in potential between the ends of the thing. So if you say "the voltage between A and B is ...", you are stating how different A is from B, the value of A relative to B.

If you say the voltage or potential "at", or "of", some (single) point, then people will assume you've defined a ground somewhere else, and that's the zero-point, relative to which you quoted this potential. So essentially, saying "the potential at X is...", you are still quoting a potential difference between two points, but one of those two points has zero potential. The other, X, is an "absolute" potential relative to zero.

I'll give you an example:

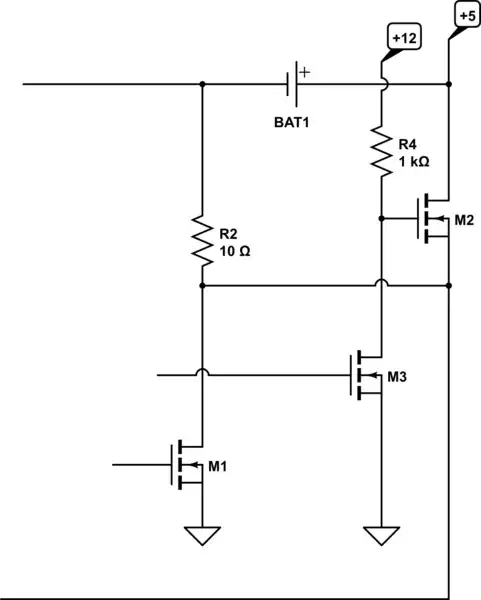
^{simulate this circuit – Schematic created using CircuitLab}

Here I am able to make the following true statements:

• The voltage across R1 is 2.3V

• The voltage across R2 is 4.6V

• The potential at S is +12V

• The voltage at node C is +7.4V, or
  The potential of C is 7.4V above ground, or
  Node C is 4.6V less than S

• The potential difference between B and E is 0.7V

• The voltage across the base-emitter junction of Q1 is 0.7V

• The potential difference between the collector and emitter of Q1 is \$V_{CE}=5.1V\$

As long as your descriptions are consistent with these ideas of absolute and difference, people will know exactly what you mean, and more importantly, if the people writing books are careful in this way, you will be able to understand them.

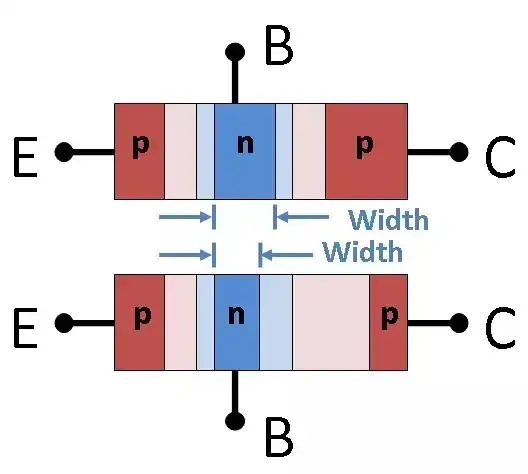
The book says that for NPN transistors the Base voltage (I'm assuming between Base and GND) has to be larger than the voltage at the Emitter (Again I think between GND)

The book says that base potential must be greater than emitter potential. These are both absolute potentials, and the statement implies \$V_B > V_E\$. You said you assume this is relative to ground, and you assume correctly. Absolute potentials are actually just potential differences between some node and 0V.

If the book had said "The potential difference between base and emitter must be greater than zero", instead, which means \$(V_B - V_E) > 0\$, this is saying the exact same thing.

The base-emitter junction can never have more than 0.7V across it, \$V_B - V_E \le +0.7V\$. When that difference is near +0.7V, then the transistor is on. Let's see if in my example above this is the case. Firstly, \$V_B=+3.0V\$, a statement saying that the base has a potential of 3V above our zero-volt ground. The emitter has a potential of \$V_E=+2.3V\$. The base is higher in potential than the emitter, the difference being \$V_{BE} = V_B - V_E = (+3.0V) - (+2.3V) = +0.7V\$.

Yes, this transistor is on.

There are two ways to switch it off. Either lower \$V_B\$ while keeping \$V_E\$ unchanged, or raise \$V_E\$ while keeping \$V_B\$ unchanged. Notice that both these actions would produce the same effect, to reduce \$V_{BE}\$ the potential difference \$V_B - V_E\$.

If there is a positive potential difference across the base-emitter junction (\$V_B - V_E > 0\$), there will be current through that junction. The emitter could be at −1000V, as long as the base is at −999.999V or above, that junction is forward biased, and current will flow. How much current depends on the difference, and is independent of potentials anywhere else in the system.

When reverse biased, the junction will block current (it's just a diode, after all). That is, with \$V_E=-1000V\$, if \$V_B\le-1000V\$ then no current will flow. I hope you see that it doesn't matter what the emitter is connected to, or what its potential is. Base current depends only on the potential of the base relative to emitter potential. It's just the difference \$V_B-V_E\$ that determine base current.

Collector current is limited by the power supply voltage, and all impedances across that supply in the path down through the collector and emitter. In my example above it is the 12V supply, and R1 and R2 that define maximum collector current.

As long as you haven't reached that maximum (the transistor is not saturated), then the transistor will have a base current according to the relationship \$I_C = \beta I_B\$. That is, it is amplifying. The subject is huge, so that's all I'll say about it here.

PNP transistors are the polar opposites of NPN. All the potential differences are reversed (\$V_{BE}=-0.7V\$, for instance), and currents flow in the opposite direction (emitter to collector). I'll redraw my circuit from above to illustrate the use of a PNP transistor to obtain the same behaviour:

^{simulate this circuit}

I swapped R1 and R2, so that R1 remains at the emitter, and I moved voltage source V2 to produce a potential 3V lower than the positive supply, +12V (as opposed to 3V greater than 0V from before). This sets base potential to +9V, and obtains a base-emitter potential difference:

$$ V_{BE} = V_B - V_E = (+9.0V) - (+9.7V) = -0.7V $$

Also, I inverted VM1. That's because I want to remain consistent with the naming conventions of potential differences in transistors. People often refer to parameter \$V_{CE}\$, which to be technically correct is defined as \$V_{CE}=V_C-V_E\$. Since collector and emitter have been swapped, I inverted VM1 to produce the correct sign:

$$ V_{CE}= V_C - V_E = (+4.6) - (+9.7) = -5.1V $$

Answer 2

Quote: "Going back to the example of 1mA at base with Beta value of 5, is the 5mA just the maximum allowed current to flow between the collector and the emitter or does it like amplify the current? I'm a bit confused."

With this post, I just want to briefly address the main misunderstanding from your question:

• There are not only the two extreme cases "collector-emitter path conductive or non-conductive", but between these two nodes E and C a current can flow, which is controlled by the voltage VBE between base and emitter. Therefore, this current can be varied in its magnitude by the signal voltage to be amplified.

• The bipolar transistor is therefore a "transconductance element" with d(IC)=gm*d(VBE). The transconductance gm is given with gm=IC/Vt. The current IB flowing into the base is - more or less - a constant part of the emitter current (IB=IE/B with IE=IC+IB), which however has no controlling effect. The current IB is simply a "by-product" that cannot be avoided.

• The maximum of the collector current IC is determined (a) either by thermal conditiones (max. current as given in the data sheet) or (b) by the voltage across the collector resistor (created by the collector current). This is because the potential at the collector must not fall below the base potential (npn case). Otherwise, the device is in saturation (no quasi-linear amplification possible).

Answer 3

Remember, voltage is always measured between two points. Regarding the BE junction, if base is at +0.7V in respect to emitter (or Gnd) the transistor is conducting.

"has to be larger than the voltage at the Emitter (Again I think between GND)"

This sentence is incorrect. There is nothing like two voltages, just one between B and E.

Answer 4

Building a conceptual amplifier

We can reveal the "transistor functionality" in the simplest way through equivalent electrical devices. I will do this in six steps by building a conceptual transistor amplifier.

Voltage-to-current converter

Basically, an amplifier should be a voltage-to-voltage converter. But for some not very clear reason (which could be discussed in another question), transistors are voltage-to-current" converters (aka "transconductance devices"). Simply put, they "produce" current at their output (at least that was what some of my students thought after taking the Semiconductor device course :-).

Let's implement this idea using the voltage controlled current source (VCCS) available in CircuitLab. I have labeled it with "gm" because this is what the "transconductance" parameter in transistors is called.

^{simulate this circuit – Schematic created using CircuitLab}

As you can see from the graph, 10 millisiemens (mS, Ω−1 or mho) means that 1 V input voltage causes 10 mA output current. Also notice that this "conceptual transistor" starts working as soon as the input voltage starts to change, ie. it is an "ideal transistor" with zero forward base-emitter voltage.

Voltage-to-current sink

The "functional transistor" above does not need power supply since, as we can see, it is a true current source containing an internal voltage source. However, real transistors do not contain such an internal source (from an energy point of view, they are passive devices that cannot generate power). All they can do is interfere with the current flowing through them. So they are "resistors" but of a more special kind - maintaining a constant current. Therefore we need to include a supply voltage source Vcc.

^{simulate this circuit}

The transfer curve is exactly the same.

Voltage-to-voltage converter with floating output

It would be good if the transistors had a voltage output, but since they failed to do it, we have to do it with the help of additional means. For this purpose, we include a resistor Rc acting as a current-to-voltage converter. The combination of the two cascaded converters acts as a composite voltage-to-voltage converter with a gain of 10.

^{simulate this circuit}

Voltage-to-voltage converter with grounded output

The problem of the conceptual amplifier above is that the load (voltmeter) is floating. But we can use the complementary voltage as an output.

^{simulate this circuit}

As a result, the circuit becomes inverting - when the input voltage increases, the output voltage decreases and vice versa.

Voltage-to-voltage converter with diode input

In these transistors, it is as if things have been swapped. Above we saw that the output of the transistor behaves as a current source but we would like it to be a "voltage source". Now we turn our attention to the input and see another quirk there - the input behaves like a voltage source (diode) which causes us a lot of problems. In some cases, this will force us to insert a base resistor Rb to "soften" the conflict with the input voltage source. We can model this input behavior by connecting a diode D in parallel to the input.

^{simulate this circuit}

The transfer curve is non-linear and we have to work with small signals.

Transistor amplifier

Now that we have a functional idea of ​​transistor behavior let's replace the "conceptual transistor" with a real one.

^{simulate this circuit}