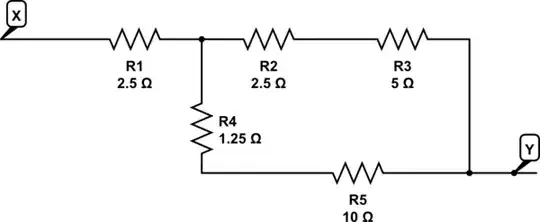
I am well aware that Thevenin voltage is equal to the open circuit voltage at the end of the circuit.
The circuit information are: \$_\$=50∠0 V, \$_\$=5∠0 A, \$_1\$=10 Ω, \$_2=10\$ Ω, and \$_=10i\$ Ω.
The circuit diagram is this:
My question is why is thevenin voltage equal to source voltage here. There should be a voltage drop cross R1 right? Can anyone help with a clear information on this?