This is the question I tried to solve.
My progress is shown in the image below. The question is how can I get another linear equation? I can't find any way. I am stuck here so it would be helpful if you could help me out.
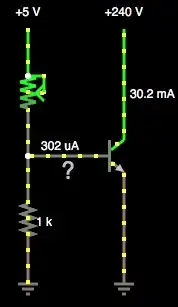
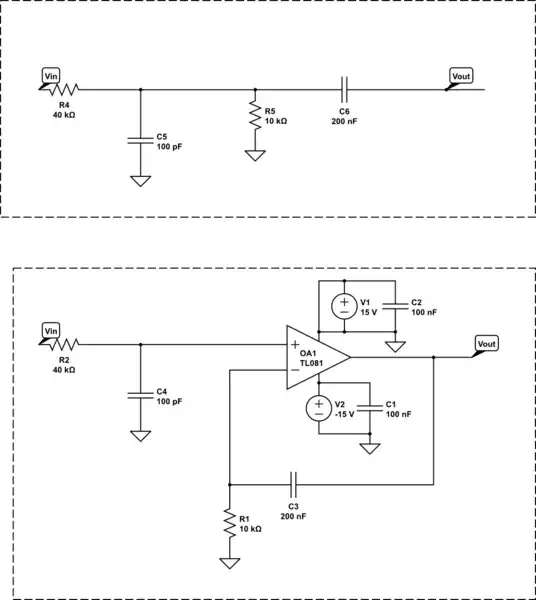
This is the question I tried to solve.

My progress is shown in the image below. The question is how can I get another linear equation? I can't find any way. I am stuck here so it would be helpful if you could help me out.


Here's the diagram, with added annotations:
We know that \$V_3=-240\:\text{V}\$ and \$I_1=19\:\text{A}\$.
We also know that \$V_3=V_1+4\cdot i_d=-240\:\text{V}\$. So \$i_d=-\frac{V_1+240\:\text{V}}{4}\$.
Also, we know that \$2\cdot i_b=I_3-I_2\$ and that \$i_b=I_4-I_2\$. So \$I_4=\frac{I_2+I_3}2\$.
So there are only \$I_2\$ and \$I_3\$ as unknown currents and \$V_1\$ and \$V_2\$ as unknown voltages.
Here are the KVL mesh equations:
$$\begin{align*} V_1-40\:\Omega\cdot\left(19\:\text{A}-I_2\right)&=0\:\text{V} \\\\ -40\:\Omega\cdot\left(I_2-19\:\text{A}\right)-5\:\Omega\cdot\left(I_2-\frac{I_2+I_3}2\right)&=V_2 \\\\ V_2-10\:\Omega\cdot\left(I_3-\frac{I_2+I_3}2\right)+240\:\text{V}&=0\:\text{V} \\\\ 4\cdot \left[-\frac{V_1+240\:\text{V}}{4}\right]-10\:\Omega\cdot\left(\frac{I_2+I_3}2-I_3\right)-5\:\Omega\cdot\left(\frac{I_2+I_3}2-I_2\right)&=0\:\text{V} \end{align*}$$
Four unknowns and four equations.
e1 = Eq(v1-40*(19-i2),0)
e2 = Eq(-40*(i2-19)-5*(i2-(i2+i3)/2),v2)
e3 = Eq(v2-10*(i3-(i2+i3)/2)+240,0)
e4 = Eq(4*(i2+i3)/2-(-240-v2)/10-10*((i2+i3)/2-i3)-5*((i2+i3)/2-i2),0)
solve( [e1, e2, e3, e4], [i2, i3, v1, v2] )
{i2: 500/19, i3: 100/19, v1: -5560/19, v2: -6560/19}
\$\therefore\quad I_4=\frac{300}{19}\:\text{A}\$.
So,
$$\begin{align*} i_a&=I_1-I_2=-\frac{139}{19}\:\text{A}\approx -7.31578947\:\text{A} \\\\ i_b&=I_4-I_2=-\frac{200}{19}\:\text{A}\approx -10.5263158\:\text{A} \\\\ i_c&=I_4-I_3=\frac{200}{19}\:\text{A}\approx 10.5263158\:\text{A} \\\\ i_d&=I_3=\frac{100}{19}\:\text{A}\approx 5.26315789\:\text{A} \\\\ i_e&=I_4=\frac{300}{19}\:\text{A}\approx 15.7894737\:\text{A} \end{align*}$$