I can't write this in a comment and it seems worthwhile to perform the algebra steps I took:
$$\begin{align*}
\frac{V_{_\text{L}}-V\left(s\right)}{R_1}+\frac{V_{_\text{L}}}{R_2}+\frac{V_{_\text{L}}}{s\,L_1}+V_{_\text{L}} s C_1 &=0
\\\\
\frac{V_{_\text{L}}}{R_1}+\frac{V_{_\text{L}}}{R_2}+\frac{V_{_\text{L}}}{s\,L_1}+V_{_\text{L}} s C_1 &=\frac{V\left(s\right)}{R_1}
\\\\
s R_1 R_2 L_1\left[\frac{V_{_\text{L}}}{R_1}+\frac{V_{_\text{L}}}{R_2}+\frac{V_{_\text{L}}}{s\,L_1}+V_{_\text{L}} s C_1\right] &=s R_1 R_2 L_1\left[\frac{V\left(s\right)}{R_1}\right]
\\\\
s R_2 L_1V_{_\text{L}}+s R_1 L_1V_{_\text{L}}+R_1 R_2 V_{_\text{L}}+s^2 R_1 R_2 L_1 V_{_\text{L}} C_1 &=s R_2 L_1V\left(s\right)
\\\\
\left(R_1 R_2 L_1 C_1 s^2 +s R_2 L_1+s R_1 L_1+R_1 R_2 \right)V_{_\text{L}}&=s R_2 L_1V\left(s\right)
\\\\
\therefore \frac{V_{_\text{L}}}{V\left(s\right)}=\frac{R_2 L_1 s}{R_1 R_2 L_1 C_1 s^2 +\left(R_1+R_2 \right)L_1s+R_1 R_2}
\end{align*}$$
You could just stop here. But there's a few standard forms for a bandpass like this that provide a little better information.
The first thing you'd want to do is to find that \$\omega_{_0}=\sqrt{\frac{b_0}{b_2}}=\sqrt{\frac{R_1 \,R_2}{R_1 \,R_2\,L_1\,C_1}}=\frac1{\sqrt{L_1\,C_1}}\$ (I use zero, not 'c' or 'p'.) You may want to highlight that fact in the resulting equation, somehow. (Yeah, \$b_2\$ is the coefficient for \$s^2\$, etc., in the denominator.)
The next thing you'd want to do is to find either the damping factor, \$\zeta\$, or else the \$Q\$. (Note: \$\zeta=\frac1{2 \,Q}\$.) It turns out that \$\zeta=\frac12\frac{b_1}{\sqrt{b_2\,b_0}}\$. (You can get \$Q=\frac{\sqrt{b_2\,b_0}}{b_1}\$, too.)
Then some standard forms are:
$$\begin{align*}
\underbrace{\overbrace{K}^{\text{gain}}\cdot\overbrace{\left[\frac{2\zeta\,\omega_{_0}s}{s^2+2\zeta\,\omega_{_0}s+\omega_{_0}^{\:2}}=\frac{\frac1{Q}\left(\frac{s}{\omega_{_0}}\right)}{\left(\frac{s}{\omega_{_0}}\right)^2+\frac1{Q}\left(\frac{s}{\omega_{_0}}\right)+1}\right]}^{\text{standard bandpass form}}}_{\text{standard bandpass form with gain}}
\end{align*}$$
To get it into that form, you need to wrestle with the numerator in order to split it up into the \$K\$ part and the \$\frac1{Q}\$ part (or \$2\zeta\$ part.)
\$\zeta\$ might be preferred over \$Q\$ when \$Q\le 1\$ with \$Q\$ preferred, otherwise. It's a matter of what shapes are of more concern, which may be picked out.
But you may be able to get away with any correct form and don't need to find standard forms.
 Edit: tried:
Edit: tried:
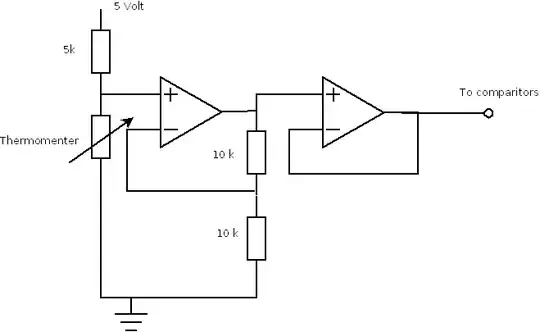 Edit: Vl/V(s):
Edit: Vl/V(s):