https://physics.stackexchange.com/questions/11799/derivation-of-self-inductance-of-a-long-wire
https://physics.stackexchange.com/questions/176783/flux-linkage-inside-of-a-conductor
https://physics.stackexchange.com/questions/734916/flux-linkage-inside-conductor
(I know that we also have to take the external magnetic field into account for a complete solution, but I am only interested in the internal contribution to self-inductance now. I also think this approximate solution is only okay assuming a homogenous distribution of current, hence low frequencies. The solution itself contradicts the assumption though.)
So many people asked the same question, yet no satisfactory answers. I tried to develop my own solution to the problem. I seek to know whether my answer is correct, and also to help other people who are also confused by this problem. First, we should remember what is self-inductance and flux linkage:
Here 5 turns (in total) induce a flux of Phi which then again cuts the 5 turns. Each turn induces an EMF of Phi' but since there are 5 turns, each one of them acts like a battery connected in series and sums to EMF = 5Phi'. Here the concept of flux linkage appears, we use Lambda=NxPhi instead of Phi and restate Faraday's law of induction as follows: Lambda = (NxPhi)' = Nx(Phi') = EMF. Hence, the EMF can be directly calculated as the derivative of the flux linkage. I prepared the following (better) illustration:
So to find the internal self-inductance of a conductor, we should calculate the flux linkage. Not flux itself. In all three questions above, OPs calculated flux spinning horizontally inside the conductor. And they did it without a mistake:
$$\phi=\frac{\mu}{8\pi}i$$
But they never did calculate the Lambda=LI to extract the self-inductance. So how shall we do it, as the number of turns is obscure here? First, let's come to the step they are stuck.
$$B_x = \mu I\frac{x}{2 \pi r^2}$$ $$d\phi = \mu I\frac{x}{2 \pi r^2} \times 1 \times dr$$
Here they are stuck. After this, they have to find
$$d\lambda = Nd\phi$$
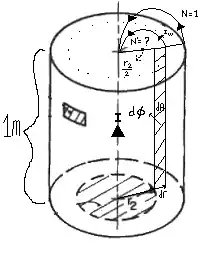
But how? I think this way: We will drive a vertical circle for the horizontal flux to flow into, an artificial turn inside the conductor, containing our flux. In practice, these artificial paths of current, correspond to the eddy currents causing the skin effect:
Iw will be our chosen path and "turn". This turn will start from the outer edge of Bx and then end at the origin. Indeed this is why current condenses on the shell of the conductor. The turn will be a circle taking x/2 as its origin.
Here dr is drawn a little bit big for an infinitesimal, and I didn't either draw the half-bottoms of the circles for a better depiction. As you can see for x=r, we have the biggest turn. We will accept that turn as N=1 and weigh other turns by their relative areas. The area for x=r is π(r/2)^2 = π(r^2)/4. This is when we have 1 turn. The area for an arbitrary x will be π(x^2)/4, and we will accept this as N = [π(x^2)/4] / [π(r^2)/4] turns which simplifies to N = (x^2)/(r^2). For example, if we take x=r/2, the number of turns can be calculated as N = 0.25
After all, we can calculate the flux linkage by taking the integral of the following equation:
$$d\lambda = Nd\phi = N(x)[B(x)dr] = \frac{x^2}{r^2}B(x)dr$$
So this is where the (x^2)/(r^2) coefficient confusing people come from, and the rest is straightforward. Is my interpretation correct?