0

Several engineers have told me that digital signal (squarewave) duty cycle can be measured accurately by comparing the amplitude of the 2nd (or 3rd - says another guy) relative to the fundamental. Neither of these engineers could give me the formula. I wrote some C code for a Nextest Lightning semiconductor tester to measure duty cycle on a 70KHz squarewave with 200ps accuracy for HP (yes, THAT HP) in Boulder, CO. Had I known this purported formula, I could have saved a lot of time. So, can you give me the formula for the ratio of the fundamental vs 2nd (or 3rd??) harmonic with 200ps of accuracy? I document the technique I developed. here

Dan Bullard
  • 11
  • 2
  • 3
    I'm curious, what is your education level / background? The solution is covered by undergrad EE (Fourier / signals analysis). Whether the "engineers" were aware of this solution (or just didn't feel committing time to looking up, deriving, or explaining it was worthwhile..) is another matter. In any case, your academic standing may be useful as a reference point for such an answer here. Also, as a rule, no one is going to want to look through a video to answer a question, but feel free to use Markdown and \$\LaTeX\$ to compile your notes here. – Tim Williams Jun 06 '23 at 01:57
  • Dan, sounds like all you care about is finding out whether or not you could have "saved a lot of time." And to see if that's the case, you want to be handed a formula without any way to independently understand or verify it because that's not what you care about. Instead you just want to see whether or not you wasted some time and the only way someone here can convince you is to show you a formula. I've no real idea. Only you do. But it comes to me like that. – periblepsis Jun 06 '23 at 02:34
  • Why not conceptually begin by simply knowing that the FT of a rectangular pulse (one pulse of some duty cycle width) is a sinc() function based upon its width? This rectangular pulse then repeats at some interval, obviously. Mathwise, that's convolution with a pulse train, a pulse train whose own FT is itself also a pulse train in the frequency domain. While considering that, also consider skimming [this slide show](https://nicadd.niu.edu/~piot/phys_630/Lesson6b.pdf). It's got all you really need to work through an answer to your own question. One that when done will be fully understood. – periblepsis Jun 06 '23 at 02:34
  • 1
    You could probably brute force it with a bunch of synthesized examples at different duty cycles and examine the spectrum to come up with a relationship or construct a lookup table such that you do not need to understand the derivation. It would be fairly simple to whip up a thousand test examples in Octave and pull out the ratio of the 1st and 3rd harmonic. You would also have to do the same with a series of frequencies and DC offsets. But accuracy is going to depend on sampling frequency, square wave frequency, sampling resolution, and noise. Math or Signal Processing SE might know. – DKNguyen Jun 06 '23 at 02:54
  • As far as saving time, that is the name of the game in production test. I wrote a test program for a Maxim ATSC TV Tuner chip. The test time was 10 seconds, and that included characterizing and fine tuning each channel (hundreds) and storing the tuning values in an on board EEPROM memory. I wrote a test program for an Analog Devices XY Accelerometer that ran 250ms, 4 times faster than AD's own home brew tester. AD said no to our tester and the head of test was so pissed over this he quit a 20 year career at AD and took a job on the west coast at another company. I hold a patent, look it up. – Dan Bullard Jun 06 '23 at 17:44

3 Answers3

3

From Andy's answer, or derived from Wikipedia equation:

https://en.wikipedia.org/wiki/Pulse_wave

enter image description here

I can't solve this for d (duty cycle) now, not sure that I ever could. But, I can plot it. The ratio of 3rd harmonic is useless, since there are 4 solutions for some ratios. The 2nd harmonic is only useful if you know that the duty cyle is less than or greater than 50%.

enter image description here

This is an interesting exercise, but I can't believe that this could ever be a better method of determining duty cycle than measuring it directly.

Edit, nice people on Math SE solved it for n = 2.

d = (1/π)arccos(r)

https://math.stackexchange.com/questions/4713624/is-this-solvable-for-d-r-frac1n-frac-sinn-pi-d-sin-pi-d

Mattman944
  • 13,638
  • 1
  • 19
  • 43
  • Useful info, thank you. It seemed to me that it was a fools errand, but I had to see if any of you agreed. My method is far superior, it just takes time to do an FFT on large data sets, and in production test, as I said, time is the enemy of productivity. – Dan Bullard Jun 07 '23 at 02:19
1

I don't know about this working well, I did a quick google and plotted the function and it looks pretty ugly in terms of sensitivity of the ratio of fundamental to 3rd harmonic to D.

Also, the ratio to the 3rd harmonic is dual valued (eg. 0.2 yields the same ratio of harmonics as 0.8, as you might expect). And there are those singularities in there.

enter image description here

Spehro Pefhany
  • 376,485
  • 21
  • 320
  • 842
  • Excellent! Thank you, that was my point exactly! 20% duty cycle and 80% duty cycle waves have EXACTLY the same spectrum, so in my mind this can never work. – Dan Bullard Jun 06 '23 at 13:26
  • The flatness of the curves (say from 0 to 0.15) also implies a lot more accuracy is required in the amplitude measurement than you expect of the D result. – Spehro Pefhany Jun 06 '23 at 13:31
1

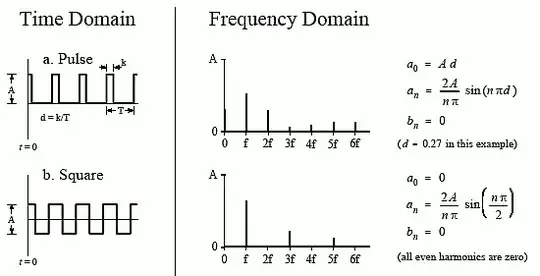
What is the formula for measuring squarewave duty cycle from a spectrum?

This is from The Scientist and Engineer's Guide to Digital Signal Processing: -

enter image description here

Andy aka
  • 434,556
  • 28
  • 351
  • 777