2

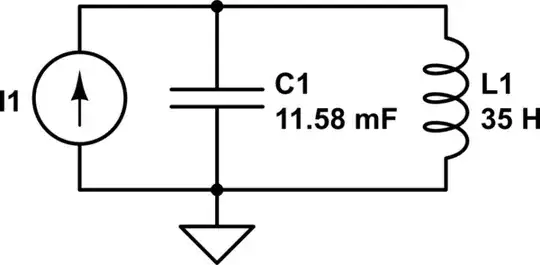
I have created a simple example in order to understand what is going on with the current through combination of resistors (parallel and in series) in a electrical circuit. I ask my self to calculate the current through resistor R3.

enter image description here

R1 is in parallel with R2 (R1||R2) and R2 in series with R3.So $$R_{eq} = \frac{5*4}{5+4}+R3 = \frac{20}{9}+8=\frac{92}{9} \approx 10.222$$.

Now the current that flows through R1 is (I use the current division here):

$$ i_{1} = \frac{i}{R_1}\left(\frac{R1*R2}{R1+R2}\right) = i\left(\frac{R2}{R1+R2}\right) =\frac{16}{3}=5.333 $$

for i_2

$$ i_{2} = \frac{i}{R_2}\left(\frac{R1*R2}{R1+R2}\right) = i\left(\frac{R1}{R1+R2}\right) =\frac{60}{9}=6.666 $$

Both currents i_1 and i_2 add up to the current that the source is giving to the circuit.And now because R3 is in series with R2 the current is the same for R3. Am I correct here? Or I am missing something?

Edit

enter image description here

winny
  • 13,064
  • 6
  • 46
  • 63
Homer Jay Simpson
  • 231
  • 6
  • 3
    All 3 are in parallel. Label your junctions and all 3 resistors are connected to both junctions. – StainlessSteelRat May 14 '23 at 18:35
  • @StainlessSteelRat I made an edit in the picture in OR but explain me why R3 is in parallel? I would appreciate it. – Homer Jay Simpson May 14 '23 at 18:45
  • 1
    @HomerJaySimpson They are still all in parallel. Rotate and move R3 next to R2 and you'll see. All three resistors connect one terminal to one node, and other terminal to the orher node. There are only two nodes. DEFGH are same node and ABC are same node. If you think R2 is in series with R3, you should explain why you think they are, because they aren't. – Justme May 14 '23 at 18:47
  • If a wire connects the junctions, they are the same junction. A junction has 3 or more wires. A, B and C are the same junction. – StainlessSteelRat May 14 '23 at 18:48
  • @Justme why?how can I say according to junctions if two resistors are in parallel or not? – Homer Jay Simpson May 14 '23 at 18:48
  • 2
    The current's going from A to H. It can go through A, B, R1, G, H. And A, B, C, R2, F, G, H. And A, B, C, R3, D, E, F, G, H. It never goes through two resistors, so none of them can be in series. – Simon B May 14 '23 at 18:51
  • @SimonB thank you for the clarification.I added another picture.Tell me if I am correct this time. – Homer Jay Simpson May 14 '23 at 18:58
  • Two ways. If you can leave one side of a resistor and go through wires to another resistor AND leave the second and go back to the first. Second, two or more resistors share two junctions. With a junction being 3 or more wires. – StainlessSteelRat May 14 '23 at 19:01
  • @StainlessSteelRat now I lost you.Your previous comment was much more helpful. – Homer Jay Simpson May 14 '23 at 19:09
  • Take a look here it may help you https://electronics.stackexchange.com/questions/511363/voltage-drop-across-a-single-resistor-and-across-two-resistors/511367#511367 – G36 May 14 '23 at 19:15
  • @HomerJaySimpson it's definitely a mixture of series and parallel in the 2nd picture. – Simon B May 14 '23 at 21:05
  • Your 1st pic and your 2nd pic are entirely different circuits. For example, in your 1st pic D, E & F are all the same node - they're joined by wires. In your 2nd pic you've grouped D % E with C, and separated F off to a different node. – brhans May 15 '23 at 15:03

2 Answers2

7

R1 is in parallel with R2 (R1||R2) and R2 in series with R3

No, that is incorrect; all three are in parallel.

Am I correct here? Or I am missing something?

The latter.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
2

Learn to redraw schematics:

schematic

simulate this circuit – Schematic created using CircuitLab

That's all it is that you have.

First, get the least common multiple of those numbers, which is 40. Use that and replace all those resistors with their whole-number conductances: \$S_1=\frac{40}5=8\$, \$S_2=\frac{40}4=10\$, and \$S_3=\frac{40}8=5\$. Sum those up to get \$S=23\$. Then the proportion of \$I_1\$ that each gets is \$\frac{S_1}{S}=\frac8{23}\$, \$\frac{S_2}{S}=\frac{10}{23}\$, and \$\frac{S_3}{S}=\frac5{23}\$.

You could use nodal and solve for the unknown voltage of that top wire and then compute the current in \$R_3\$, too.

(The Rank-Nullity Theorem explains exactly why there's no need to connect the other side of \$I_1\$ to anything and why there's no need to separately do KCL for the ground node. In fact, the mathematics won't work if you do write KCL for ground. But that's another topic.)

periblepsis
  • 3,766
  • 1
  • 1
  • 10