Simulating a tuning circuit in LTspice

Question

This is the tuning circuit that I'm trying to simulate in LTspice:

My input signal is the sum of a 500 kHz, 1 MHz, and 1.5 MHz sine wave, all modulated at 5 kHz. The 5 kHz waves carried by each of the frequencies are 90 degress apart from each other, as demonstrated in the equation of my input signal below:

\begin{align} f_\text{1 MHz}(t) &= \cos(2\pi.10^6t).[1+\cos(2\pi.5000t)] \\ f_\text{500 kHz}(t) &= \cos(2\pi.500{\times}10^3t).\left[1+\cos\left(2\pi.5000t+\frac{\pi}{2}\right)\right] \\ f_{1\cdot5\text{ MHz}}(t) &= \cos(2\pi.1{\cdot}5{\times}10^6t).\left[1+\cos\left(2\pi.5000t-\frac{\pi}{2}\right)\right] \\ f_\text{signal}(t)&=f_\text{1 MHz}(t)+f_\text{500 kHz}(t)+f_{1\cdot5\text{ MHz}}(t) \end{align}

From what I understand, L1 and C1 should short the 500 kHz and 1.5 MHz signal respectively and only the 1 MHz signal would be present across the output load R2, but when I simulate my circuit using the input signal I described above and have a look at the output signal in both the time and frequency domains, that doesn't seem to be the case:

For reference, here's what the input signal looks like the the time and frequency domains:

Does anyone know why the 500 kHz and 1.5 MHz signals aren't getting filtered?

Answer 1

You have made a low Q or wideband filter. Increase R1 to sharpen it up. Try 10K then 100K.

Answer 2

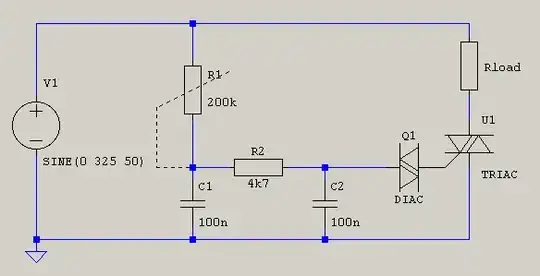
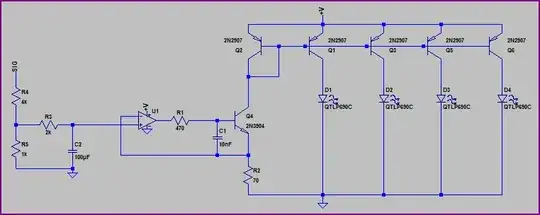
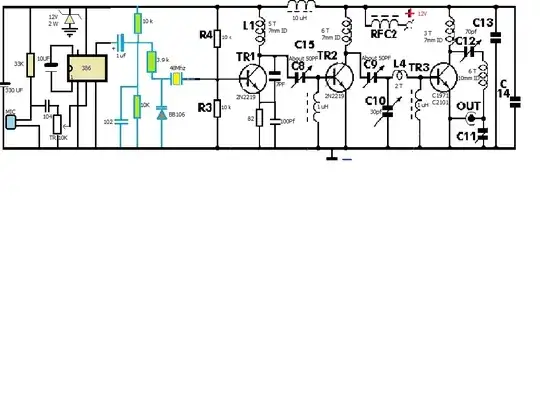
Well, let's analyze this circuit. The transfer function is given by:

\begin{equation} \begin{split} \mathscr{H}\left(\text{s}\right)&=\frac{\text{V}_\text{o}\left(\text{s}\right)}{\text{V}_\text{i}\left(\text{s}\right)}\\ \\ &=\frac{\displaystyle\text{sL}\space\text{||}\space\frac{\displaystyle1}{\displaystyle\text{sC}}\space\text{||}\space\text{R}_2}{\displaystyle\text{R}_1+\left(\text{sL}\space\text{||}\space\frac{\displaystyle1}{\displaystyle\text{sC}}\space\text{||}\space\text{R}_2\right)}\\ \\ &=\frac{\displaystyle\frac{\displaystyle1}{\displaystyle\frac{\displaystyle1}{\displaystyle\text{sL}}+\frac{\displaystyle1}{\displaystyle\frac{\displaystyle1}{\displaystyle\text{sC}}}+\frac{\displaystyle1}{\displaystyle\text{R}_2}}}{\displaystyle\text{R}_1+\frac{\displaystyle1}{\displaystyle\frac{\displaystyle1}{\displaystyle\text{sL}}+\frac{\displaystyle1}{\displaystyle\frac{\displaystyle1}{\displaystyle\text{sC}}}+\frac{\displaystyle1}{\displaystyle\text{R}_2}}}\\ \\ &=\frac{\displaystyle\text{LR}_2\text{s}}{\displaystyle\text{CLR}_1\text{R}_2\text{s}^2+\text{L}\left(\text{R}_1+\text{R}_2\right)\text{s}+\text{R}_1\text{R}_2} \end{split}\tag1 \end{equation}

Where \$\displaystyle\alpha\space\text{||}\space\beta\space\text{||}\space\gamma=\frac{\displaystyle1}{\displaystyle\frac{\displaystyle1}{\displaystyle\alpha}+\frac{\displaystyle1}{\displaystyle\beta}+\frac{\displaystyle1}{\displaystyle\gamma}}\$.

When working with sinusoidal inputs we know that we can write \$\text{s}:=\text{j}\omega\$ where \$\text{j}^2=-1\$. So we get:

\begin{equation} \begin{split} \left|\space\underline{\mathscr{H}}\left(\text{j}\omega\right)\right|&=\displaystyle\left|\frac{\displaystyle\text{LR}_2\text{j}\omega}{\displaystyle\text{CLR}_1\text{R}_2\left(\text{j}\omega\right)^2+\text{L}\left(\text{R}_1+\text{R}_2\right)\text{j}\omega+\text{R}_1\text{R}_2}\right|\\ \\ &=\displaystyle\frac{\displaystyle\left|\text{LR}_2\text{j}\omega\right|}{\displaystyle\left|\text{CLR}_1\text{R}_2\cdot\text{j}^2\cdot\omega^2+\text{L}\left(\text{R}_1+\text{R}_2\right)\text{j}\omega+\text{R}_1\text{R}_2\right|}\\ \\ &=\displaystyle\frac{\displaystyle\text{LR}_2\omega}{\displaystyle\left|\text{R}_1\text{R}_2-\text{CLR}_1\text{R}_2\omega^2+\text{L}\left(\text{R}_1+\text{R}_2\right)\omega\text{j}\right|}\\ \\ &=\displaystyle\frac{\displaystyle\text{LR}_2\omega}{\displaystyle\sqrt{\left(\text{R}_1\text{R}_2-\text{CLR}_1\text{R}_2\omega^2\right)^2+\left(\text{L}\left(\text{R}_1+\text{R}_2\right)\omega\right)^2}}\\ \\ &=\frac{\displaystyle\text{LR}_2\omega}{\displaystyle\sqrt{\left(\text{R}_1\text{R}_2\left(1-\text{CL}\omega^2\right)\right)^2+\left(\text{L}\left(\text{R}_1+\text{R}_2\right)\omega\right)^2}} \end{split}\tag2 \end{equation}

Now, let's analyze a few cases:

1. \$\omega\space\to\space0\$: $$\lim_{\omega\space\to\space0}\left|\space\underline{\mathscr{H}}\left(\text{j}\omega\right)\right|=0\tag3$$
2. \$\omega\space\to\space\infty\$: $$\lim_{\omega\space\to\space\infty}\left|\space\underline{\mathscr{H}}\left(\text{j}\omega\right)\right|=0\tag4$$
3. When is \$\left|\space\underline{\mathscr{H}}\left(\text{j}\omega\right)\right|\$ at a maximum: $$\frac{\partial\left|\space\underline{\mathscr{H}}\left(\text{j}\hat{\omega}\right)\right|}{\partial\hat{\omega}}=0\space\Longleftrightarrow\space\hat{\omega}=\frac{1}{\sqrt{\text{CL}}}\tag5$$

So, we get:

$$\left|\space\underline{\mathscr{H}}\left(\text{j}\hat{\omega}\right)\right|=\frac{\text{R}_2}{\text{R}_1+\text{R}_2}\tag6$$

So, the cut-off frequency is:

$$\left|\space\underline{\mathscr{H}}\left(\text{j}\omega\right)\right|=\frac{1}{\sqrt{2}}\cdot\left|\space\underline{\mathscr{H}}\left(\text{j}\hat{\omega}\right)\right|\space\Longrightarrow\space$$ $$\omega_\pm=\frac{\displaystyle\sqrt{\frac{\text{L}\left(\text{R}_1+\text{R}_2\right)^2+\text{C}\left(2\text{R}_1\text{R}_2\right)^2}{\text{L}}}\pm\left(\text{R}_1+\text{R}_2\right)}{\displaystyle2\text{CR}_1\text{R}_2}\tag7$$

So, the bandwidth is given by:

$$\mathcal{B}:=\left|\omega_+-\omega_-\right|=\frac{\text{R}_1+\text{R}_2}{\text{CR}_1\text{R}_2}\tag8$$

And the quality factor is given by:

$$\mathcal{Q}:=\frac{\hat{\omega}}{\mathcal{B}}=\frac{\displaystyle\frac{1}{\sqrt{\text{CL}}}}{\displaystyle\frac{\text{R}_1+\text{R}_2}{\text{CR}_1\text{R}_2}}=\sqrt{\frac{\text{C}}{\text{L}}}\cdot\frac{\text{R}_1\text{R}_2}{\text{R}_1+\text{R}_2}\tag9$$

Notice that in your case your bandwidth is equal to: $$\mathcal{B}=\frac{4010000000}{127}\space\text{rad/sec}=\frac{2005000000}{127 \pi }\space\text{Hz}\approx5.02529\space\text{MHz}\tag{10}$$ Which is way too broad.

Answer 3

As pointed out by @Autistic, your filter is too "broad" ...