While measuring loop gain using AP300 frequency analyzer, why we always focus on loop gain involving control to output transfer function?
Is it because input to output transfer depends on power stage and not important for controller design?
(If there is a variation in input, it will result in variation at output and eventually variation in control parameter)
Why we always focus on loop gain involving control to output transfer function?
Theoretically you can break the loop at any point to measure loop gain. However, what you must avoid is breaking the loop at a point that changes the loop gain i.e. if you choose to break the loop at a point of high source impedance loaded by an input of low-ish impedance then, unless you were very careful at recreating those impedance-loading scenarios, when the loop is broken, you will get into trouble for sure.
And, conveniently, the output has a low impedance and the feedback resistors have a much higher impedance hence, that point is naturally suitable for loop-gain measurement.
A switching regulator can be described by the below block diagram. The input of this control system is the reference voltage, in the left side, while the output is \$V_{out}\$. The input voltage \$V_{in}\$ and the output current \$I_{out}\$ are perturbations the converter must fight. There is the audio-susceptibility (the ability to reject the perturbation coming from \$V_{in}\$) and the current absorbed by the load which reduces the output voltage because of the open-loop output impedance:
In a switching regulator, the reference voltage is fixed and sets the dc operating point. In small-signal analysis, because its level does not change while you ac-modulate the system, it does not play a role and it is 0 V in ac. You are left with a control system that we call a regulator: what the system does is deliver a constant output voltage (or current sometimes) permanently fighting the perturbations: if \$V_{in}\$ changes, you want \$V_{out}\$ to remain constant and if the load draws more current, you also want \$V_{out}\$ to remain unaffected.
For implementing this strategy, the system needs gain: no gain, no feedback. When I say "no gain" it means that the system, beyond crossover, runs ac open-loop: if you have a 10-kHz perturbation on the input voltage while crossover is 1 kHz, the system will do what it can to fight it but it virtually runs open-loop in ac.
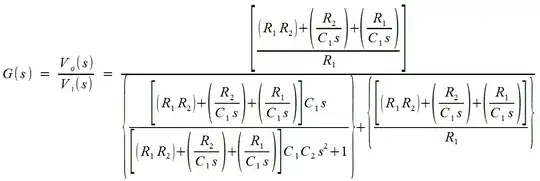
The above expression describes how the output voltage is determined based on the perturbations inputs. You can see that the key to the rejection is the open-loop gain \$T\$. This gain involves the control variable, the duty ratio \$D\$ and that is the one the loop will act upon when correcting perturbations. The relationship linking a stimulus applied on the control input \$D\$ with the response observed on \$V_{out}\$ is the control-to-output transfer function you need to determine (bench measurement, simulation or analytical analysis) before thinking of a compensation strategy (poles and zeroes in the compensator). It is the one determining the way the control system will react to a change in the perturbation. Measuring the transfer function between \$V_{out}\$ and \$V_{in}\$ would certainly tell you how efficiently the system rejects incoming perturbation but it won't directly tell you about stability.
