1

I would like to run an AC analysis with a voltage source whose voltage varies with frequency according to the following piecewise plot:

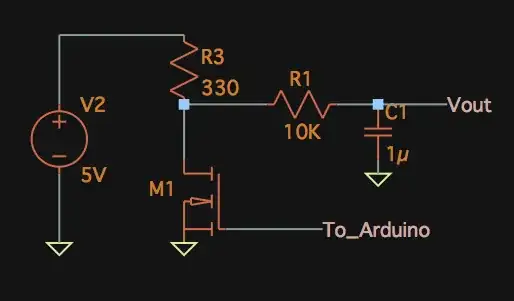
enter image description here

I've heard it's impossible to have a frequency dependent voltage source in LTspice. I'm able to get around this for the first part of this curve using this technique:

enter image description here

Above, B1's voltage increases with frequency at 20dB/decade, just like the first part of the piecewise voltage function I'm going for. The second part is of course very simple - just a standard small signal AC voltage source.

I'm struggling with the third part of the piecewise, as there's no simple circuit I know of that creates a voltage that falls off at -10dB/decade. Furthermore, I'm not sure how to integrate these various sources into one piecewise source. I could brute force this by having three separate sims, one for each source, but I would prefer a more elegant solution. Any tips on these issues?

Ste Kulov
  • 3,771
  • 10
  • 22
burkesm2
  • 23
  • 4
  • 1
    What do you expect to gain from varying the voltage in an AC analysis? It's a linear analysis so you might as well just scale the output, unless I'm missing something. – Spehro Pefhany Apr 25 '23 at 22:02
  • @SpehroPefhany I have a diode, BJT, and MOSFET in my sim. Are they treated as linear for the purpose of an AC analysis? – burkesm2 Apr 25 '23 at 22:38
  • 1
    That is my understanding. The algorithm finds the operating point and linearizes about that operating point, and scales based on the claimed input amplitude. – Spehro Pefhany Apr 25 '23 at 23:29
  • Yes, the `.ac` simulation is a small signal analysis which implies linearization. See the built-in LTspice page for the `.ac` command ([web archive version here](https://ltwiki.org/LTspiceHelpXVII/LTspiceHelp/html/AC_analysis.htm)). I think you had a bit of an XY problem going on. Anyway, sounds like you just need to use a FREQ table. I'll post an answer for you. – Ste Kulov Apr 26 '23 at 03:36

1 Answers1

1

I've heard it's impossible to have a frequency dependent voltage source in LTspice.

I don't know where you heard this from. Anyway, I believe you just need to use a "FREQ table", which is simply a way to make a piecewise-linear source in the frequency domain. It's not in any of the official LTspice documentation, but LTspice can do it since it touts PSpice model compatibility and this feature is originally a PSpice feature.

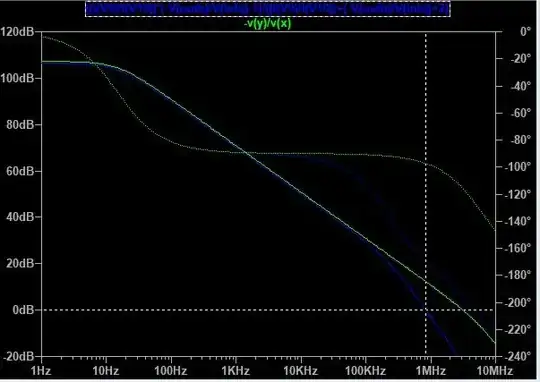
Here is an example that plots your desired frequency response: enter image description here

In this example consisting of only 4 points it's easy to define the FREQ table directly on the component within the schematic. If your target function requires a bunch more points, it might be easier to define the component as a SPICE directive and have it as a text block off to the side using the + symbol to allow you to continue a super long line horizontal line vertically (see the last entry of the first table here). If it's even BIGGER, then it's probably better throwing it into a subcircuit and .lib-ing it into the simulation. The answers to this previous question tackle some of that more nuanced stuff if you're interested:

LTspice: tables for parameterized passive components... why not?

It's worth noting that you can also define much smoother curves in the frequency domain using the Laplace feature. Both FREQ and Laplace suffer from artifacts when used in transient simulations because LTspice has to compute an IFFT to get the impulse response. However, Laplace is usually more well-behaved in that respect. If you're just doing .ac analysis, then you don't have to worry about that aspect, but if necessary more info can be found in the LTspice Help under "B. Arbitrary Behavioral Voltage or Current Sources" (duplicated below):

If an optional Laplace transform is defined, that transform is applied to the result of the behavioral current or voltage. The Laplace transform must be a function solely of s. The Boolean XOR operator, ^, is understood to mean exponentiation, **, when used in a Laplace expression. The frequency response at frequency f is found by substituting s with sqrt(-1)2pi*f. The time domain behavior is found from the sum of the instantaneous current(or voltage) with the convolution of the history of this current(or voltage) with the impulse response. Numerical inversion of a Laplace transfer function to the time domain impulse response is a potentially compute-bound process and a topic of current numerical research. In LTspice, the impulse response is found from the FFT of a discrete set points in frequency domain response. This process is prone to the usual artifacts of FFT's such as spectral leakage and picket fencing that is common to discrete FFT's. LTspice uses a proprietary algorithm that exploits that it has an exact analytical expression for the frequency domain response and chooses points and windows to cause such artifacts to diffract precisely to zero. However, LTspice must guess an appropriate frequency range and resolution. It is recommended that the LTspice first be allowed to make a guess at this. The length of the window and number of FFT data points used will be reported in the .log file. You can then adjust the algorithm's choices by explicitly setting nfft and window length. The reciprocal of the value of the window is the frequency resolution. The value of nfft times this resolution is the highest frequency considered. Note that the convolution of the impulse response with the behavioral source is also potentially a compute bound process.

Ste Kulov
  • 3,771
  • 10
  • 22
  • Fantastic, thank you! This isn't necessary, but do you know if there's any way to combine the FREQ table and Laplace functions? Like let's say I want the BV source to be defined by a FREQ table from 10kHz to 10Meg, then by a Laplace function from 10Meg to 100Meg. – burkesm2 Apr 27 '23 at 15:49
  • @burkesm2 Hmmm...I don't believe so as the `FREQ` command overrides the `Laplace` command. The best workaround I can think of is to simulate your 10Meg to 100Meg section using Laplace, and then take the datapoints and export them into a FREQ table which you can add to the end of your existing 10k to 10Meg table. So you're kind of "sampling" the Laplace function in a sense and using the samples to extend your table. If you want finer resolution, run your "sampling" simulation at a higher points per decade. Go to [File]->[Export data as text]. You might have to use Notepad++ to add `+` signs. – Ste Kulov Apr 28 '23 at 06:33
  • @burkesm2 Here's a quick example. B1 is a full Laplace function. B2 is your original table. B3 is made using a SPICE directive. It's made using the table data from B2 from 10k to 10Meg PLUS data from a previous run of B1 from 10Meg to 100Meg. Result of B3 is plotted as `V(out3)`. https://i.stack.imgur.com/Zr8Vz.png – Ste Kulov Apr 28 '23 at 06:38
  • 1
    That makes sense, I'll give that a try soon. Thanks again!! – burkesm2 May 01 '23 at 17:31