LLC ZVS deadtime calculation

Question

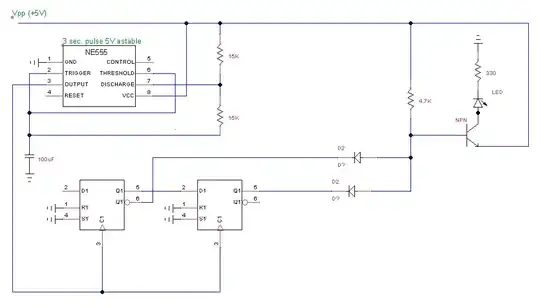
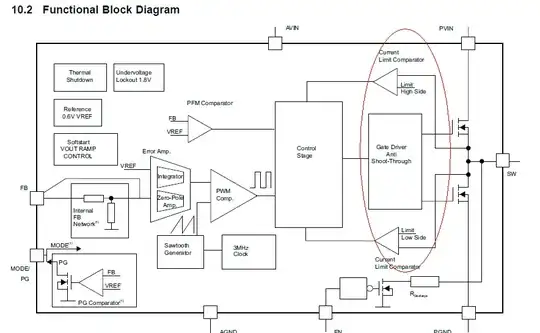
According to the TI LLC document, I can use eq 32 to calculate the dead time to achieve the ZVS in the half-bridge LLC Converter.

below is my spec of half bridge of LLC converter.

the deadtime I calculated value is around 452ns. but when I use this value and run the simulation, I think the dead time is too much. the Vds2 is already zero. I am confused about why eq 32 can't match the simulation.

Simulation result:

But amperage is not a phase angle... What matters is drain current at the instant of commutation. Note the relation is equal *or greater* so it's not clear what your confusion is about; the value seems perfectly adequate. — Tim Williams, Apr 15 '23 at 17:17

score 1 · Accepted Answer · answered Apr 15 '23 at 14:35

1

I have run the calculation in my seminar on the LLC converter and the results are shown below for a 245-kHz switching frequency and two fixed 120-pF parasitic capacitors:

So, approximately, the zero-voltage switching or ZVS condition would be met in 34 ns or so when the half-bridge transitions. Let's check with the ready-made template you can download here:

The transition is realized in 31 ns which is well in par with the calculation. A deadtime of 40-50 ns would then do the job nicely.

In your simulation, check that you are well in steady-state condition and have a look at the peak magnetizing current which should be routed in these capacitors for proper operation.

answered Apr 15 '23 at 14:35

Verbal Kint

20,420
1
16
50

Hi I have checked the waveform is stable. I update the waveform here. what do you mean by the peak magnetizing current which should be routed in these capacitors for proper operation. – Power JJ Apr 15 '23 at 14:50
In my simulation, the ZVS only needs 300ns. but the calculated value is 452ns I think the range is too big. – Power JJ Apr 15 '23 at 14:53
I try to use your ready-made template, and using my spec, the result is the same as mine. – Power JJ Apr 16 '23 at 00:56
Try to measure the peak magnetizing current and compare it with the expression given for \$I_m\$. The amount of current in these caps determines their discharge/charge times. Then check which in the expressions that I used in the illustration deviates significantly from what is expected. – Verbal Kint Apr 16 '23 at 07:26
Ok, I knew it. it seems misunderstand something in there. – Power JJ Apr 16 '23 at 07:30

LLC ZVS deadtime calculation

1 Answers1