I have an ESP32 with a DAC pin that outputs a variable voltage between 0 and 3.3 V.
I need to convert this signal to another voltage range: between -15 and +15 volts. This signal need to drive around 1 A (the more the better).
What is the best way to achieve this in the simplest possible way?
Note: the output pin of the ESP32 does not have to be DAC, it can also be PWM, SPI, I2C, etc. if it makes the solution simpler.
You want to translate 0 V to 3.3 V to -15 V to 15 so you need to offset and scale.
The scale is what you need to bring the input voltage range to the output voltage range.
$$ \frac{15V - (-15V)} {3.3V - 0V} = \frac{30}{3.3} = 9.09...$$
The offset is what you need to bring the low input voltage down to the low output voltage, so -15 V in this case. If you do the offset before the scaling you can make the offset -1.65 V, since you want your signal centered at 0 V and 1.65 V is half of 3.3 V.
You can use a subtractor circuit with gain of 9.09... to subtract 1.65 V from your input voltage. the resistor ratio for that gain is 100:11, so we'll use 100k and 11k. A simple divider will get the 1.65 V reference from the micro's 3.3 V supply, two 22k resistors will give us an equivalent of 11k. The output of the opamp can be buffered with some transistors to get more current, I've used a simple class B arrangement here. The opamp could be a different type, with a rail-to-rail one you could lower Vcc and Vee. The output is into a 15\$\Omega\$ load so the current is +/-1 A. Note that the buffer is in the feedback loop.
The relationship you require between input and output is:
$$ \begin{aligned} V_{OUT} &= \frac{15}{1.65} \times (V_{IN} - 1.65) \\ \\ &= V_{IN} \times 9.09 - 15 \\ \\ \end{aligned} $$
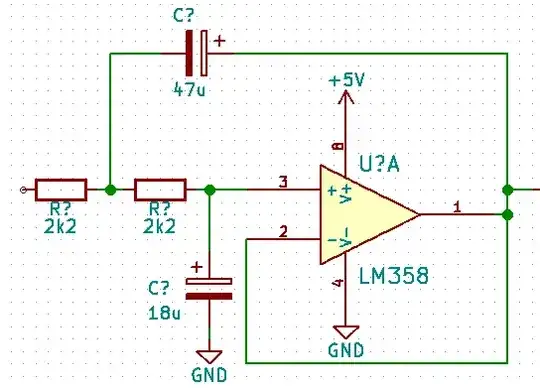
Consider this design:
simulate this circuit – Schematic created using CircuitLab
It has the relationship:
$$ \begin{aligned} V_{OUT} &= V_{IN1}\left(1 + \frac{R_2}{R_1}\right) - V_{IN2}\frac{R_2}{R_1} \\ \\ \end{aligned} $$
Those last two equations have the same form (something times \$V_{IN1}\$ minus something times \$V_{IN2}\$), and these terms can be equated:
$$ \begin{aligned} 1 + \frac{R_2}{R_1} &= 9.09 \\ \\ V_K \frac{R_2}{R_1} &= 15 \\ \\ \end{aligned} $$
The first one allows us to choose some resistances whose ratio is 9.09. If I arbitrarily set \$R_1 = 10k\Omega\$, then \$R_2\$ is:
$$ \begin{aligned} R_2 &= (9.09 - 1)R_1 \\ \\ &= 81k\Omega \\ \\ \end{aligned} $$
\$V_K\$ is some constant potential whose value is:
$$ \begin{aligned} V_K &= 15\frac{R_1}{R_2} \\ \\ &= 1.85V \end{aligned} $$
Plugging all these values into our amplifier, we get:
That produces the desired offset and amplification:
There's just the little problem of not having a source of 1.85V, so assuming you have a 3.3V source, we can make one with a pair of resistors as a potential divider. The only issue is that if we replace source V2 with this derived 1.85V, then connect R1 to it, the total impedance of R1 and our divider will be greater than 10kΩ, messing up our carefully engineered gain.
However, if we can make a resistor potential divider with equivalent source impedance of 10kΩ then we can dispense with R1, and replace it altogether with our divider. In other words, we need to create a potential divider, which together with a 3.3V source, will have a Thevenin equivalent exactly like V2 and R1 above:
There are two conditions. Firstly, the values R3 and R4, if combined as if they were in parallel, should be 10kΩ. Secondly, the voltage at the junction of R3 and R4 should be +1.85V. These two conditions are written algebraically like this:
$$ \begin{aligned} \frac{R_3 \times R_4}{R_3 + R_4} &= 10k\Omega \\ \\ 3.3V \times \frac{R_4}{R_3 + R_4} &= 1.85V \end{aligned} $$
I won't show my working to solve these equations for R3 and R4, but they are:
$$ \begin{aligned} R_3 = 17.8k\Omega \\ \\ R_4 = 22.8k\Omega \\ \\ \end{aligned} $$
Replacing R1 and V2 with the equivalent:
If you use a power op-amp, like the PA74 there may be nothing more to do, except take care of heating. Maximum power dissipation will happen when the load is sinking/sourcing 1A, and has half the total supply across it, 20V. That's \$P=IV=20W\$, and will require beefy heat-sinking, and probably forced-air cooling.
If you don't have a power op-amp, and can't get one, then you'll have to build your own buffer stage, to produce the same voltage, but capable of sinking and sourcing 1A. Here I will do this with a push-pull arrangement consisting of bipolar transistors.
A typical BJT has a current gain of about 100, which would require 10mA of base current in order to source/sink 1A. That's really at the edge of what we can ask of your average op-amp, so I'll use darlington pairs to increase current gain, and relieve the op-amp of any significant current demand. You'll need an op-amp capable of outputting at least ±17V to get the full ±15V output swing:
The buffer stage is placed inside the op-amp's feedback loop, so that it's getting feedback from the buffer's output instead of its own. This kind of setup can be quite unstable, and oscillate somewhat (especially with a capacitive load). I try to mitigate this with C1 for some frequency compensation, but this is probably insufficient. You'd need to do some serious stability analysis, and employ better frequency compensation than this.
R5 protects the op-amp by preventing it sourcing or sinking its maximum short-circuit current in the event you do something silly at the output.
Also there's a huge dead-zone near 0V out, where neither transistor is on, which could lead to instability, and will definitely cause crossover distortion, but that's way to deep to go into here.
Q2 and Q4 can get very hot, since they could potentially dissipate 20W. This is the price you pay for a linear power stage like this, with such a large output voltage range and high current capability. They must be mounted on big heat-sinks, and probably cooled with a fan.
Here's the output (orange) of that circuit when a sinusoidal input (blue) varying from 0V to 3.3V is applied at IN
