Is every linear circuit equivalent to a single series RLC circuit? If not, can one determine from the transfer function of the linear circuit whether or not it is equivalent to a single series RLC circuit; that is to say, what form (zeroes and poles) must the transfer function of a single series RLC circuit take/satisfy?
-
There's as many as one state for each L (current through it) and for each C (voltage difference across it) and for each moment of time. An RLC can only have at most two such states. – periblepsis Apr 02 '23 at 20:55
-
@periblepsis should you not add "independent" after "for each"? – Sredni Vashtar Apr 02 '23 at 21:08
-
@SredniVashtar Perhaps. I thought I had that covered with the "as many as." But one can always write more and/or better. Granted. The basic point remains and was all I had intended to get across at the time. – periblepsis Apr 02 '23 at 21:19
-
You mentioned zeros and poles, so I'll add this: All transfer functions of the form \$\frac{a_ms^m+a_{m-1}s^{m-1}+\dots+a_1s+a_0}{b_ms^m+b_{m-1}s^{m-1}+\dots+b_1s+b_0}\$ can be handled by [this general active filter block](https://i.stack.imgur.com/0831K.png) using only R's and C's. (Technically, just four active elements are required, using pairs of amplifiers with positive and negative gains, because all the remaining \$K_{{\small IN}_i}\$ and \$K_{{\small OUT}_i}\$ can be created using passive attenuators.) Picture from Sallen-Key paper, TR-50, 1954. – periblepsis Apr 03 '23 at 02:34
2 Answers
Is every linear circuit equivalent to a single series RLC circuit?
No. All passive linear circuits can be reduced to an order that is dependent on the number of independant storage elements. They can be all capacitors, all inductors, or a combination of the two. There is no general requirement that an n-th order circuit must contain both L and C
I assume the diagram is what you are referring to: This circuit is a 2nd order circuit, because there are 2 independent storage elements L and C.
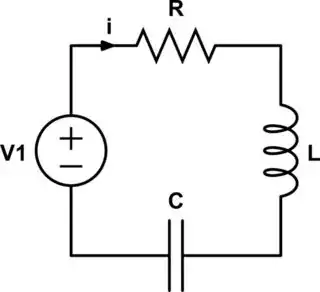
simulate this circuit – Schematic created using CircuitLab
what form (zeroes and poles) must the transfer function of a single series RLC circuit take/satisfy?
There is not a single transfer function for this circuit, but there is a single characteristic polynomial for the circuit.
A transfer function is defined as the ratio of an output to an input. There is one input, but there are 7 possible outputs: \$v_R\$, \$v_L\$, \$v_C\$,\$(v_R+v_L\$), \$(v_R+v_C\$), \$(v_L+v_C\$), and \$i\$, the circuit current. So there are seven possible transfer functions. For example:$$\frac{V_L(s)}{V_1(s)}=\frac{s^2}{s^2+\frac{R}{L}+\frac{1}{LC}};\frac{V_L(s)+V_C(s)}{V_1(s)}=\frac{s^2+\frac{1}{LC}}{s^2+\frac{R}{L}+\frac{1}{LC}}$$
Notice that the denominator is the same and will be for all transfer functions for the same circuit and so is called the characteristic polynomial (CP).
By applying the quadratic formula to the CP, the poles can be found. The zeros can be found in the numerator.The transfer functions can be written in pole-zero form as:$$\frac{V_L(s)}{V_1(s)}=\frac{(s+j0)(s-j0)}{(s-p_1)(s-p_2)};\frac{V_L(s)+V_C(s)}{V_1(s)}=\frac{(s+j\omega _0)(s-j\omega _0)}{(s-p_1)(s-p_2)}$$
Other 2nd order circuits can have two independent capaitors, or two independant inductors. Or parallel RLC or other combinations.
All second order circuits can be reduced to a single second order form. Series RLC circuits do not represent anything other than series RLC circuits
$$G(s)=\frac{N(s)}{s^2+2\zeta \omega_Ns+\omega^2_N}$$
where \$\zeta\$ is the damping ratio and \$\omega_N\$ is the natural frequency (angular velocity)
The numerator \$N(s)\$ varies depending on which output is being used, but the CP will be the same for all second order circuits.
The poles are:$$p_1,p_2=-\zeta\omega_N\pm\omega_N\sqrt{\zeta^2-1}$$
The zeros are dependent on the form of the numerator.
Additional remark: The above discussion assumes that the resistors, inductors and capacitors are time invariant (constants).
As TimWescott mentioned in a comment, all n-th order passive systems must have their poles on the left side of the Laplace plane. If any are not, then either the system is not a passive linear time-invariant system, or there is an error.
- 12,496
- 2
- 9
- 34
-
2"They can be all capacitors, all inductors..." I'm not sure how you meant that, but you can't take any arbitrary transfer function and implement it as resistors and just capacitors or just inductors. The transfer function cannot have any poles in the right-half plane, and it cannot have any resonant poles -- to realize resonant pole pairs in a passive circuit, you need both capacitors and inductors. – TimWescott Apr 02 '23 at 22:33
-
2@TimWescott:"can't take any arbitrary transfer function and implement it as resistors and just capacitors or just inductors.". True. But there is no general requirement that an n-th order circuit must contain both L and C, Resonance is not implied in the question and so I did not treat it. – RussellH Apr 02 '23 at 22:45
-
So, the denominator "encodes the dynamics of the system" while the numerator "encodes the observed variable(s)" (at least, that's the way I think about with (A,B,C,D) state-systems). That really clears things up, thanks! – Jeffrey Rolland Apr 03 '23 at 21:45
-
1@JeffreyRolland: Yes. The denominator comes from the output variable, which in turn comes from the system state. While the numerator is different for different outputs, the numerator derives from the input side also. The TF represents the system whether or not the signals are present . – RussellH Apr 03 '23 at 21:59
While it is sufficient to note that "series RLC" is not equivalent to "linear circuit", a stronger statement can also be made: there are linear circuits which are not equivalent to lumped-element (RLC) circuits of any topology and finite size. Examples are generally distributed wave systems and other transport phenomena: transmission lines, diffusion (ionic diffusion in batteries, electromagnetic diffusion in metals (skin effect)), etc.
Such systems can, however, be approximated reasonably well with finite networks. A transmission line can be represented exactly with infinite poles at infinity, or quadratically many at some multiple of the required bandwidth (that is, quadratic with the delay time (electrical length) of the line); or a diffusion (Warburg) element with a geometric series of poles (distributed along the real axis).
- 22,874
- 1
- 20
- 71