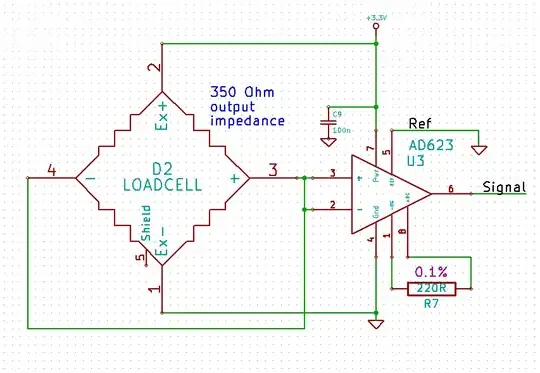
I would like to know how to set minimum system bandwidth according to the following requirement :
I have a system regulating an output. In nominal operation, the system has to regulate its output to \$S_{out1}\$. Then when an event occurs, the system change its reference (input) in order to change its output. The new output is \$S_{out2}\$.
The time required for changing from \$S_{out1}\$ to \$S_{out2}\$ is \$t_{out1->out2}\$. (Suppose the system takes no time for detecting the event).
My idea was to think about a sinewave and at the derivative around 0 where the slope of the sinewave is maximal in order to extract the frequency of the sinewave and so the bandwidth
\$f(t) = Asin(2*Pi*f*t)\$
And then,
\$f = \frac{slope}{2*Pi*A}\$
But it depends on the amplitude of the sinewave and it is not a parameter that I really know. So it makes me think that it is a bad approximation.