Find the equivalent resistance

Question

I have to simplify the following circuit by using equivalent resistance. I know it probably should be very simple to do it, but for some reason, I can’t tell if the two resistors in the “internal” mesh are in series or in parallel with the other resistor R, in the external mesh.

MY GUESS

I was able to simplify the circuit only to this point, by using the fact that:

• There is a short circuit between node a and node b
• The two resistors in the internal mesh are equivalent to one resistor of resistance 2R, since they are in series

My question is: are these two in series or in parallel? I would say in parallel, but the fact that there is just one node confuses me, I think.

Answer 1

You did well. You can imagine that the dot in parallel with 2R is a wire. In other words they are shorted.

However, normally, an equivalent resistance is usually taken between 2 nodes (sometimes, one of them is ground). In your network, after getting rid of the 2R, I still see a loop of wire in parallel with R. In that case, I'd say the total R of the network is 0.

Answer 2

I'll try to follow a straightforward approach, directly from the initial schematic.

Between a and b there are three paths in parallel:

• the wire connection at the top,
• the two R resistors in the "internal mesh",
• the one R resistor in the "external mesh".

(If you have difficulty seeing that fact, it helps to "pull" at the two points, a to the left and b to the right, treat the wires as rubber bands, and watch how the elements re-arrange.)

The resistances on these three paths are:

• 0
• 2R
• R

Any parallel circuit where one path has zero resistance gives zero resistance, so the result is zero.

Answer 3

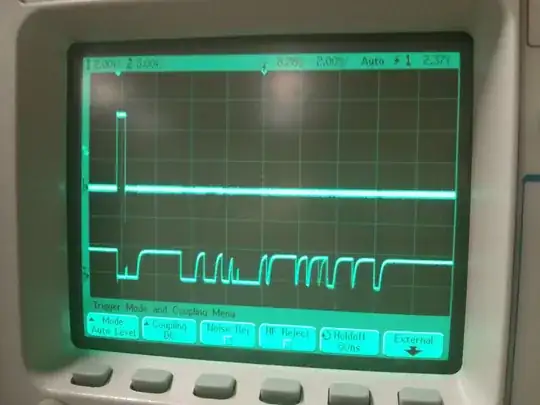
I have to simplify the following circuit by using equivalent resistance.

If the only things you're interested in happen "between a and b", then the question and the suggested approach are misleading at best, and nonsense at worst.

Nodes in circuit analysis are abstract things. The connected lines don't mark wires - they mark nodes. So, if letters "a" and "b" are on the same connected line, they denote the same node, and by definition a node has no (zero) resistance to itself.

The entire line with letters "a" and "b" on it is just one node. The letters are a distraction.

Whatever is connected to this node doesn't matter at all. There could be no circuit at all, or an arbitrarily complex circuit. From the point of view of circuit analysis - and that's what you're doing here - there's one node of interest only.

Trying to apply some reasoning that would treat "a" and "b" nodes as being separate may be an interesting thought exercise but is pointless until they actually become separate, not just two names for one node!

So, to apply any sort of equivalent resistance analysis, there must be two nodes to have resistance between. How can we do that? We must split the "ab" node into two nodes "a" and "b", and add a "shunt" resistance between them. Like this:

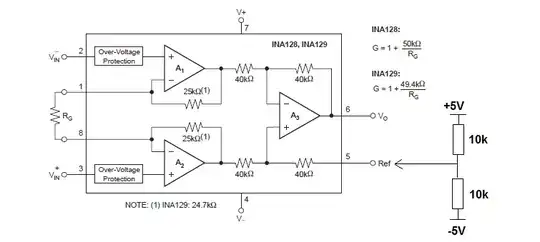
^{simulate this circuit – Schematic created using CircuitLab}

Now we can actually use equivalent resistance, because there are two nodes!

The circuit reduces to \$R_s\$ we just added, in parallel with "the rest of the circuit", i.e. \$\frac{2}{3}R\$. The resistance between "a" and "b" $$ R_{ab} = \left(\frac{2}{3}R \right)||R_s = \frac{(2/3)R\cdot R_s}{(2/3)R + R_s} = \frac{R\cdot R_s}{R + (3/2)R_s}.$$ We can now ask "what happens as \$R_s\$ goes to zero?" $$ \lim_{R_s\to 0} \frac{R\cdot R_s}{R + (3/2)R_s} = \frac{R\cdot 0}{R+0} = 1\cdot0 = 0.$$

You can see that the impedance of the entire circuit beyond \$R_s\$ doesn't matter - it can be whatever, can be complex, imaginary, even nonlinear (as long as it's finite).

So, we don't even need to figure out what the equivalent impedance of the rest of the circuit is. We could just call it \$R_x\$, and see if we need to know it. We don't: the math is the same, the result is independent of \$R_x\$: $$ \lim_{R_s\to0}R_{ab}=\lim_{R_s\to0} R_x||R_s = \lim_{R_s\to0} \frac{R_x\cdot R_s}{R_x+R_s} = \frac{R_x\cdot0}{R_x+0} = 0 \text{ iff } R_x\ne0. $$

The simple substitution limit-taking method doesn't apply when \$R_x=0\$. De l'Hospital's rule to the rescue: $$ \lim_{R_s\to0}R_{ab} = \lim_{R_s\to0} \frac{R_x\cdot R_s}{R_x+R_s} \overset{\rm DH}{=} \lim_{R_s\to0} \frac{\frac{d}{dR_s} (0\cdot R_s)} {\frac{d}{dR_s} (0+R_s)} = \lim_{R_s\to0} \frac{0}{1} = 0.$$

^{simulate this circuit}