0

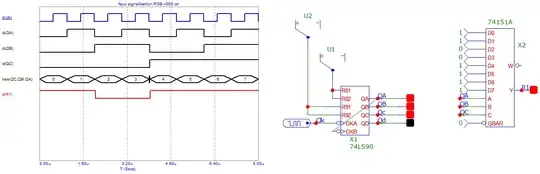
Assuming a simple binary state variable allocation can be made and that any unused states can be treated as don’t cares. How would I Design a corresponding transition table for this system including flip-flop (D- FF) inputs and system inputs/outputs. (I am unsure why the table looks so weird outside of the editor its my first time using this). Here is the State table:

State Clock A B C R1 Y1 G1 R2 Y2 G2 Output
S0 5s 0 0 0 1 0 0 1 0 0 S1
S1 6s 0 0 1 1 1 0 1 0 0 S2
S2 80s 0 1 0 0 0 1 1 0 0 S3
S3 6s 0 1 1 0 1 0 1 0 0 S4
S4 5s 1 0 0 1 0 0 1 0 0 S5
S5 6s 1 0 1 1 0 0 1 1 0 S6
S6 80s 1 1 0 1 0 0 0 0 1 S7
S7 6s 1 1 1 1 0 0 0 1 0 S0

I have tried this 3 times and got it wrong three times any help would be greatly appreciated.

My attempt:

State D0 D1 C0 C1 R1 Y1 G1 R2 Y2 G2
S0 0 0 0 0 1 0 0 1 0 0
S1 0 0 1 0 1 1 0 1 0 0
S2 0 1 0 0 0 0 1 1 0 0
S3 0 1 1 0 0 1 0 1 0 0
S4 1 0 0 0 1 0 0 1 0 0
S5 1 0 0 1 1 0 0 1 1 0
S6 1 0 1 0 1 0 0 0 0 1
S7 1 0 1 1 1 0 0 0 1 0

(D0 and D1) represent the binary state variable allocation. (C0 and C1) represent the system inputs/outputs.

Emoanimelovr
  • 1
  • 1
  • How would i design a transition table from this state table? – Emoanimelovr Feb 03 '23 at 17:25
  • looks like a homework assignment – Roland Feb 03 '23 at 17:27
  • its a self project assignment since I'm studying electronics alone I have done the Karnaugh and VHDL myself I also built the logic system but I cant get the excitation or transition maps correct and I don't know where I am going wrong – Emoanimelovr Feb 03 '23 at 17:28
  • Edited with my try of the transition table – Emoanimelovr Feb 03 '23 at 17:36
  • 3
    Seems that these are traffic lights ... – Antonio51 Feb 03 '23 at 17:59
  • yes they are traffic lights ns ew traffic lights i got this project from a book called Computer Organization and Architecture An Introduction by B. S. Chalk it was one of the last few projects and i just cant build the transition table or excitation map since i don't understand those concepts at all the i don't know how to take this data and apply it to a d flip flop that's why i am asking for help (step by step help if possible) but the answer would also be appreciated as the book doesn't include any answers to any problems given – Emoanimelovr Feb 03 '23 at 18:43
  • You can note also that "states" are the numbering of an "up-counter". And R1Y1G1 ... are just a "combination" of each state (can be each synthesized by a multiplexor). – Antonio51 Feb 03 '23 at 20:19
  • You need just do the "table transition" with "actual" state (first column) and the future state (last column) of the "state table". And then apply D-FF rules ( need 3). Timers not used. – Antonio51 Feb 04 '23 at 13:59

1 Answers1

0

See this note for reference.

So, the problem is "synthetizing" a "counter" ... with D-FF, and you need 3 D-FF.
Your second table is not what you are "searching" ...

...

When "counter" will be synthesized ...,
you should be able to draw a circuit like this (this is only the beginning ... and a "fast" version.

Only the first "light" is drawn (R1). You should do the same for other lights.
NB: the timing is not included, only the "sequence". Should use also some timers.
The 74151 is used as a "general" function of 3 variables (can be "extended").

enter image description here

Antonio51
  • 11,004
  • 1
  • 7
  • 20