1

I am designing a board with an FT232H chip to communicate through USB (bus powered configuration). The oscillator configuration is described in the datasheet, with the pertinent section pasted below.

I believe I have the parallel capacitor selection under control, but am puzzled by the lack of specification of the drive level for the crystal in the FT232H datasheet. I see suitable crystals available with drive level of 10-100 μW, or 100-1000 μW, for instance. This diagram also shows no damping resistor, which I find puzzling.

How do I know what the drive level range of the crystal I choose should be?

I suspect that this crystal (12 MHz version. 10-100 μW, ESR = 60 Ω) might be appropriate. I would like to understand if this would be a good choice and why (or why not). I lack experience designing crystal circuits, so detail would be much appreciated.

enter image description here

ocrdu
  • 8,705
  • 21
  • 30
  • 42
ron19
  • 107
  • 5
  • 1
    It's a weak section within the chip document but, you can make some observations on paper that predict the power will be less than about 250 uW (given the crystal you picked). However, the xtal you picked is maxing out at 100 uW so, you need to find one that has the full equivalent circuit specified if you want to do this accurately. – Andy aka Jan 18 '23 at 19:09
  • Thank you. I may have to follow up on that comment with a separate question. But first I want to spend some more quality time with the excellent page on your [website](http://www.stades.co.uk/XTAL%20Oscillator/XTAL%20Oscillator.html). – ron19 Jan 18 '23 at 20:36
  • Well spotted/found. Look at the impedance graph of the "10 MHz" crystal and notice that the oscillation point will be slightly higher (maybe 10.001 MHz) and that means it has an impedance of about 1000 ohm. That is basically how you can find a pretty close value for the power used. On a 3.3 volt supply, the RMS voltage applied from the output will be about 1 volt and, that means there can be no more than 1 mA flowing. If the series resistance of the xtal is 60 ohm (power dissipative component) then the power is 60 uW as an estimate. – Andy aka Jan 18 '23 at 21:08
  • 1
    After studying your comment and your web page, I understand much better how all this works. The web page is a really excellent resource -- thanks for putting that out there. – ron19 Jan 18 '23 at 22:54
  • 1
    About the (lack of) damping resistor...this chip designer may have made the assumption that small low-power 12 MHz crystals would be used. For this limited range, he/she can tailor the oscillator's transconductance to a fairly narrow range suitable to drive small crystals. To accommodate a wide-range of crystals, higher \$g_m\$ would be designed-in, and then you'd need a damping resistor for low-power xtals. You *might* find this oscillator balky if you try larger HC-49 crystals that specify a larger load capacitance, or 12MHz ceramic resonators having low impedance. – glen_geek Jan 19 '23 at 15:12

2 Answers2

2

If you really want to know, you need to measure the crystal current. It's not hard but requires care and fairly expensive instrumentation (or lots of your time). This video by the late Jim Williams explains what's involved in the measurement.

The FTDI folks could get some drive power value out of their SPICE model of the oscillator circuit, assuming they have one and aren't just reusing an oscillator cell that someone else designed. The accuracy of that would depend on having an accurate SPICE model of the exact crystal you're using, since it's only the combination of the two that would determine the exact drive level achieved.

In my experience, you can pray or measure - no two ways about it, absent a specification in the datasheet of the IC that has the oscillator circuit in it. That's why I generally stay away from discrete crystals and use integrated oscillators. They cost a bit more, but I can be sure their internal crystal or MEMS resonator is driven at an appropriate level and will perform up to spec.

You need to be selling a lot of your devices for there to be any real savings from using a crystal vs. an oscillator. The time you've already spent thinking about it would have paid for a lot of oscillators :)

Kuba hasn't forgotten Monica
  • 32,734
  • 1
  • 38
  • 103
  • Thank you, very helpful. Cost is not an issue. I have seen a design with the FT232H using a discrete crystal, which I was mimicking somewhat to reduce my risk of failing, but the part number of the crystal was not available to me. Could you foresee any other potential side effects of switching to an integrated oscillator, such as having to configure the EEPROM differently that is used with this FT232H, or other requirements? – ron19 Jan 18 '23 at 19:07
  • 1
    FTDI has probably an app note about using external oscillators. Some chips default to internal clock source. Usually oscillators have an explicit input and output. As long as the input is driven with something - even a sine wave - it will work. It’s a very common thing to do - in all of my designs you’d see oscillator going via a small series resistor to XIN on the chip. The series resistor is optional - I tweak it to minimize clock leakage through the MCU/ASIC pins, on a custom test setup. In most cases you can put some reasonable value and it’s fine - like 20 or 47 ohms. – Kuba hasn't forgotten Monica Jan 19 '23 at 13:44
  • An alternative approach for the series resistor determination is to use a low capacitance FET probe to observe the XIN waveform with the crystal attached - ideally on an evaluation board provided by the ASIC vendor. Save that as a reference on the scope, then tweak the series resistor on your oscillator-based design to get similar signal amplitude (a bit higher to be safe). This is for improving electromagnetic compatibility only, most of the time. The series resistor can be 0R if you don’t want to mess with it. Still can be “rolled back” if EMI troubles arise related to the particular clock. – Kuba hasn't forgotten Monica Jan 19 '23 at 13:49
  • I appreciate your comments and help. I am going to look for such an app note from FTDI. – ron19 Jan 19 '23 at 16:25
1

A while ago I did a bit of a tear-down on crystals and crystal oscillators. I looked at the equivalent circuit of a crystal and put some notes on my basic web-site.

I have to mention the source of pictures to keep within site rules

I analysed a few different 10 MHz crystal data sheets and "contrived" an equivalent circuit of a typical device that has a series resonant frequency of exactly \$\color{red}{\text{10.000000 MHz}}\$.

The series resonant frequency is not the oscillation frequency; it's close but, it's not the same (more later)

If the crystal was used in a Pierce oscillator, it would oscillate a shade higher at around 10.001 MHz and, if this "contrived" crystal were a real device it would be marked 10.001 MHz. Example of a Pierce oscillator if you were to build it from scratch: -

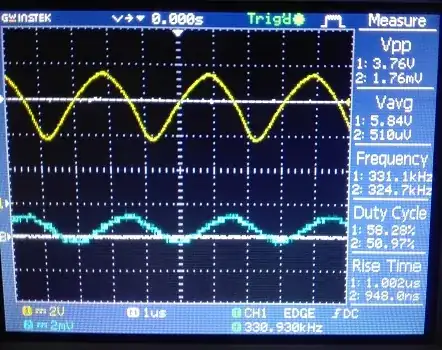
enter image description here

If you took the "contrived" 10.001 MHz crystal and plotted its impedance it would look like this: -

enter image description here

And, as I said before, it would oscillate at about 10.001 MHz despite it being series resonant at 10.000000 MHz (more later on why). At 10.001 MHz you can see that the crystal has an impedance of about 1000 Ω (and is in the inductive section of the graph).

Because it presents an impedance of 1000 Ω, we can calculate the current flowing though it based on the drive voltage from the OSCOUT terminal. We would normally consider the OSCOUT terminal to be a 3.3 volts p-p square wave. However, because of the output capacitor (27 pF) and the internal output resistance of the inverting gate, it will be a bit lower and more sine shaped.

I estimate that the drive voltage hitting the crystal will be about 1 volt RMS.

Given that the crystal has an impedance of 1000 Ω and there is another 27 pF capacitor to ground at OSCIN, we can calculate the full loading impedance to be around 1100 Ω (1000 Ω + Xc).

This means a crystal current of 909 μA and, a power through the internal resistance of the crystal (60 Ω) of 50 μW.

Anyway, the bit that shows the crystal operates slightly higher than the series resonant frequency: -

enter image description here

Adding the input and output capacitors makes the voltage phase shift through the circuit 180° at a frequency slightly higher than 10.000000 MHz. The internal silicon in the chip is an inverter and, that adds another 180° phase shift hence, the total phase shift around the loop is 360° (equivalent to 0°) and, it will oscillate.

OK, the crystal shown in the question is a 12 MHz type but the principle is the same, it will have an operating impedance of around 1000 Ω. But, it's still an imperfect analysis so, the only way to resolve this is to ask the supplier for the crystal's equivalent circuit and simulate it. Or measure it if you are so inclined.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
  • Thank you for the excellent details. Your website was extremely helpful too. Based on what I learned studying that, it seems like there must be series resistance built into the FT232H chip.....otherwise, it would be hard to get enough phase shift for stable oscillation, correct? Wouldn't I need to know that value to model the circuit properly even if I had the crystal equivalent circuit? – ron19 Jan 19 '23 at 01:36
  • 1
    @ron19 to model it properly yes but, it's likely to be around 20 ohms for an oscillator that runs in the MHz region. I can only say that most chip suppliers and most crystal suppliers are very lax about providing good information to the interested user. At the other end of the scale (such as wrist watch 32.768 kHz oscillators), the output series resistor can and will be many tens of kΩ to keep power levels low. – Andy aka Jan 19 '23 at 08:33