0

I have a 4th order transfer function. Given transfer function is below.

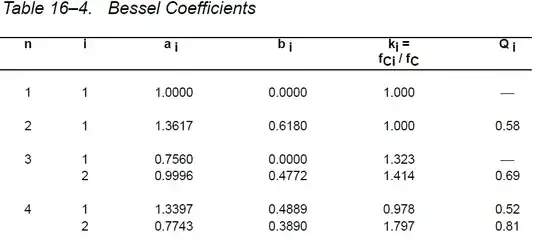
enter image description here

If given transfer function had been 2nd order transfer function, it would easily be factorization of transfer function like:

[2]: https://i.stack.imgur.com/SebWL.png

How could be written like above format for 4th order transfer function? I will be appreciated for help. Thanks in advance.

bcdyzi
  • 89
  • 4
  • It is a complicated exercise and usually people find an approximation which is good enough to approach the response of the complicated 4th-order polynomial. Have a look at this [document](https://docplayer.net/19018047-Bode-diagrams-of-transfer-functions-and-impedances-ecen-2260-supplementary-notes-r-w-erickson.html) (page 21) which discusses how to factor coefficients. Where does your transfer function come from? – Verbal Kint Jan 10 '23 at 06:41
  • It may or may not help, but I notice the coefficients in the denominator are 1, sqrt(3), 3, sqrt(3), 1. Just sayin'. – Neil_UK Jan 10 '23 at 06:46
  • The transfer function come from Bessel Polynomial. @VerbalKint – bcdyzi Jan 10 '23 at 07:10
  • No idea if the goal is supposed to be symbolic factorization, or approximating, or plotting the response, or what; but you might reflect upon what 1.732^2 is near, and see about making use of that fact. Mind, root loci are notoriously unstable with respect to coefficients, so this isn't a great place for approximation in general. – Tim Williams Jan 10 '23 at 07:29
  • @bcdyzi No, that's not from a Bessel. The factored 2nd order Q's are wrong for that. – periblepsis May 04 '23 at 03:05

3 Answers3

0

You can algebraically factorize 4th order equations, such as shown here: https://math.stackexchange.com/questions/3282632/how-to-factor-a-fourth-degree-polynomial

An easier way of doing it (if you don't have to show your work on paper) is calculating the zeros of the transfer function with a root-finding method (calculator) and representing the denominator of the transfer function as all of those "zero terms" being multiplied. For example, your transfer function has roots: at -0.548+/-1.192j and -0.318+/-0.692j. Therefore, the denominator will be: (s+0.548+1.192j)(s+0.548-1.192j)(s+0.318+0.692j)(s+0.318-0.692j)

Microcontroller Enjoyer
  • 145
  • 6
0

The transfer function come from Bessel Polynomial.

The Bessel filter can be broken down into two stages using coefficient tables. The tables have been produced and reproduced in many sources such as this one: -

enter image description here

I don't know the original source because it came from this question that I answered.

So, for a 4th order Bessel you get two lots of coefficients and these relate to two 2nd order stages having TFs like this: -

$$A_i(s)=\frac{A_0}{1+a_is+b_is^2}$$

If you multiplied both TFs together I'm sure you'd get something similar to what your equation is.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
0

If you plot the denominator on a graphing calculator or using MATLAB or similar tools, you can find the roots (R1, R2, R3, R4) for the denominator of the polynomial.

Once you know the roots you can then use a technique called Partial Fraction Expansion to re-write the original equation as the sum of several fractions.

$$T_s=\frac{s^2}{s^4+1.732s^3+3s^2+1.732s+1}=s^2(\frac{A}{s-R_1}+\frac{B}{s-R_2}+\frac{C}{s-R_3}+\frac{D}{s-R_4})$$

Finding the numerators is simple. To find A, multiply both sides of the equation by (s-R1) and then evaluate at s = R1.

$$T_s * (s-R_1)=s^2(A+\frac{B(s-R_1)}{s-R_2}+\frac{C(s-R_1)}{s-R_3}+\frac{D(s-R_1)}{s-R_4})$$

At s = R1, all the (s - R1) terms will equal 0 so most of the equation disappears. We are then left with...

$$T_s * (s-R_1)=s^2A$$

So...

$$A = \frac{T_s(R1)*(s-R_1)}{S^2} $$

Note that because Ts has (s-R1) as a root in its denominator, the (s-R1) term will cancel out and the result is not usually zero.

You can repeat that process to find numerators B, C, D the same way as for finding A.

user4574
  • 11,816
  • 17
  • 30