Why does this metallic magnetic core have so little core losses up until 100s of kHz?

Question

I have a small signal transformer with values as in the below schematic (the simulate button works well to see the AC response). The values are measured and the simulated AC response agrees sort of well with the actual behavior. In case anyone wonders about the large value of C1: It is the capacitance from two antiparallel protection diodes.

The loss resistances R2/R3 turned out so high that the signal essentially isn't attenuated at all (that's good... don't get me wrong). I expected them to be "lower" (more lossy) because of the highly conductive core material.

The core is made from VITROPERM 500F (see tables at the bottom of this page for parameters).

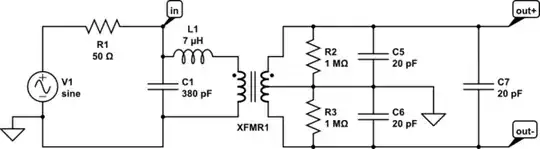
^{simulate this circuit – Schematic created using CircuitLab}

The core loss mechanisms in transformers that I am aware of are:

• magnetic hysteresis losses, which is the dominant loss mechanism for high resistivity ferrites up until very high frequencies
• eddy current losses which should be rather large in VITROPERM, as its resistivity is only about 100x that of copper (5-6 orders of magnitude lower than usual ferrites)

So VITROPERM should be really lossy even at intermediate frequencies due to eddy losses, and indeed the company VAC seems to be proud of the high lossiness of VITROPERM for applications such as common-mode chokes. For example Fig. 7 in that document shows how VITROPERM is already very lossy in the dozens of kHz:

Judging from that graph, I would expect that the inductive behavior of the core essentially gives way to a dissipative one already at ~40 kHz and that magnetic coupling between primary and secondary should be greatly attenuated as a result.

Still I see two things which I guess shouldn't happen: I could also see the resonance of the leakage inductance L1 with the secondary capacitances at ~250 kHz. And for lower source impedance R1, I could also transmit much higher frequencies, 100s of kHz, without attenuation.

So why is it, that metallic transformers are considered way too lossy for SMPS, but this transformer with a metallic core, transmits just fine up until 250 kHz?

Answer 1

Take a look at this cross section of a tape-wound core from https://www.magneticmetals.com/products-materials/tape-wound-toroidal-cores :

I have added the arrow to show the direction of the eddies that will result from your windings. Notice that the eddy currents must cross many layers of the Vitroperm tape. Each layer of tape is insulated from its adjacent layers as it is wound on, so the eddy path is interrupted.

As you go up in frequency, the eddies get smaller until eventually you can have significant eddies within the thickness of a single layer of tape. But, tape-wound cores use tapes with thicknesses of less than a mil; 0.5 mil thicknesses are common (0.0127 mm). So, the tape reduces eddy currents in the same fashion as laminations in larger transformers, and their upper frequency is dependent on the thickness of the tape.

Answer 2

Vitroperm is not a metallic material, it's an nanocrystalline alloy (ultra fine grains of FeSi are embedded in Nb and Cu additives). Transformers made of this type of materials are commonly used in SMPS

Answer 3

TL;DR

From a quick research I made on the Internet, the explanation may lie in the material being made of nanoparticles.

Explanation

Although eddy current losses in bulk magnetic materials increase with frequency, as stated in Wikipedia here, from an excerpt from a book here we infer that nanoparticles behave differently (copy-pasted as image because of lots of formulas):

_{Source: "Design Criteria of Thermal Seeds for Magnetic Fluid Hyperthermia From Magnetic Physics Point of View"; Hiroaki Mamiya, Balachandran Jeyadevan, in "Nanomaterials for Magnetic and Optical Hyperthermia Applications", 2019}

Note the last sentence (emphasis mine):

It is evident that, in reality, for magnetic particles in nanosize range, eddy current loss can be ignored in comparison with the hysteresis loss, although it plays a major role in the case of bulk magnetic material placed on top of IH cooker.

This would explain why, that material behaves like it is advertised.

The fact that the material is also manufactured in tiny sheets would further decrease eddy current losses, as lamination do in good old mains transformers with EI-core made of FeSi alloy.

EDIT

Further research led me to this article:

The influence of Fe nanoparticles on microstructure and magnetic properties of Fe-6.5wt%Si soft magnetic composites

excerpt (emphasis mine):

Abstract

The effect of Fe nanoparticles with mass fraction of 0-7 wt% on the microstructure and soft magnetic properties of the Fe-6.5 wt%Si soft magnetic composites (SMCs) was investigated. The results show that the pores between Fe-6.5 wt%Si powders can be effectively filled by Fe nanoparticles, thereby correspondingly increasing the density of the SMCs. At the same time, the magnetic permeability of the SMCs mixed with different mass fraction of Fe nanoparticles has improved significantly and exhibits good frequency stability compared with the absence of Fe nanoparticles. It also reveals that the addition of 1 wt% Fe nanoparticles can reduce the eddy current loss of the SMCs by decreasing its intra-particle eddy current loss. When the addition of Fe nanoparticles is 3 wt%, the SMCs exhibits good magnetic properties with high magnetic permeability (increased by 24%) and relatively low core loss.

which further support my hypothesis.

Answer 4

Simple: the magnetizing inductance doesn't play much role in the LL-Cs resonance. Core loss is effectively in parallel with the magnetizing current, i.e. the primary or secondary inductance. If the magnetizing current is small enough -- you really don't care what phase it has!

^{simulate this circuit – Schematic created using CircuitLab}

This is a typical 2nd order nonideal transformer model. Rp/Rs model DC resistances, Cp/Cs the total winding self-capacitances (there will also be some across the isolation barrier, between the respective ends of the windings), LLp/LLs the leakage inductance (for \$k \rightarrow 1\$, we can approximate it by lumping it all to one side; at lower \$k\$, we might want to use both), Lm the magnetizing inductance, and Rm its loss. T1 is an ideal transformer with ratio N2/N1.

As a first order model, core loss can be represented simply as a resistance in parallel with the magnetizing inductance.

This approach is also the trick with RF transformers: it's hard to find any material that's meaningfully inductive (not loss dominant) at 100s of MHz, but simply using enough turns that the magnetizing impedance is several times the system impedance (i.e., say 200 ohms compared to the 50 ohm transmission line it connects to) gets you there with <1dB insertion loss, and if that's good enough, who cares, eh?

It may be worth noting that fringing fields and leakage flux (the flux literally leaking out of the core, into space -- not necessarily just that measured between windings) flow thru-plane in these materials (high-mu amorphous/nano. materials are made in strip form only), so will encounter high losses. This is really only a problem with uneven windings, or around air gaps.

Uneven windings includes the sectoral wind on a toroid, such as commonly used for common mode chokes. In that case, the differential mode will have higher losses. (But, that's not at all a problem in that application; it might be valuable if anything.)

These materials are also available in cut C cores, which can be air-gapped for inductor use (energy storage). This isn't useful at high frequencies for this reason; but the low losses at mains frequency may still make them useful (if a rather expensive choice).