How can I calculate the transfer function of a low-pass Sallen–Key filter?

Question

I was looking at the following circuit. AFAIK, this is a low-pass Sallen–Key filter, with a VCVS instead of the op-amp.

I started to work out the transfer function, but somehow I got lost at a certain step.

First, you can use the common node to state:

$$V_{A}(s)=V_{1}(s)$$ and $$V_{D}(s)=\mu V_{C}(s)=V_{2}(s)$$ then the KCL for nodes at \$V_b\$ and \$V_C(s)\$:

$$\frac{V_{B}(s)-V_{1}(s)}{R_{1}}+\frac{V_{B}(s)-V_{C}(s)}{R_{2}}+\frac{V_{B}(s)-\mu V_{C}(s)}{\frac{1}{C_{1}s}}=0$$ $$\frac{V_{C}(s)-V_{B}(s)}{R_{2}}+\frac{V_{C}(s)}{\frac{1}{C_{2}s}}=0$$

multiplicating by \$R_{1}R_{2}\$ $$\frac{R_{1}R_{2}(V_{B}(s)-V_{1}(s))}{R_{1}}+\frac{R_{1}R_{2}(V_{B}(s)-V_{C}(s))}{R_{2}}+\frac{R_{1}R_{2}(V_{B}(s)-\mu V_{C}(s))}{\frac{1}{C_{1}s}}=0$$

$$\frac{R_{1}R_{2}(V_{C}(s)-V_{B}(s))}{R_{2}}+\frac{R_{1}R_{2}(V_{C}(s))}{\frac{1}{C_{2}s}}=0$$

$$R_{2}(V_{B}(s)-V_{1}(s))+R_{1}(V_{B}(s)-V_{C}(s))+\frac{R_{1}R_{2}(V_{B}(s)-\mu V_{C}(s))}{\frac{1}{C_{1}s}}=0$$

$$R_{1}(V_{C}(s)-V_{B}(s))+\frac{R_{1}R_{2}(V_{C}(s))}{\frac{1}{C_{2}s}}=0$$

$$R_{2}V_{B}(s)-R_{2}V_{1}(s)+R_{1}V_{B}(s)-R_{1}V_{C}(s)+\frac{R_{1}R_{2}V_{B}(s)}{\frac{1}{C_{1}s}}-\frac{R_{1}R_{2}\mu V_{C}(s)}{\frac{1}{C_{1}s}}=0$$

$$R_{1}V_{C}(s)-R_{1}V_{B}(s)+\frac{R_{1}R_{2}V_{C}(s)}{\frac{1}{C_{2}s}}=0$$

$$R_{2}V_{B}(s)-R_{2}V_{1}(s)+R_{1}V_{B}(s)-R_{1}V_{C}(s)+C_{1}sR_{1}R_{2}V_{B}(s)-C_{1}sR_{1}R_{2}\mu V_{C}(s)=0$$

$$R_{1}V_{C}(s)-R_{1}V_{B}(s)+C_{2}sR_{1}R_{2}V_{C}(s)=0$$

$$(R_{1}+R_{2}+R_{1}R_{2}C_{1}s)V_{B}(s)-(R_{1}+\mu R_{1}R_{2}C_{1}s)V_{C}(s)=R_{2}V_{1}(s)$$

$$(R_{1}+R_{1}R_{2}C_{2}s)V_{C}(s)=R_{1}V_{B}(s)$$

$$(R_{1}+R_{2}+R_{1}R_{2}C_{1}s)V_{B}(s)-(R_{1}+\mu R_{1}R_{2}C_{1}s)V_{C}(s)=R_{2}V_{1}(s)$$

$$R_{1}(1+R_{2}C_{2}s)V_{C}(s)=R_{1}V_{B}(s)$$ $$\frac{R_{1}(1+R_{2}C_{2}s)V_{C}(s)}{R_{1}}=\frac{R_{1}V_{B}(s)}{R_{1}}$$

$$(1+R_{2}C_{2}s)V_{C}(s)=V_{B}(s)$$

From the schematic you can tell

$$V_{2}(s)=\mu V_{C}(s)$$

$$(R_{1}+R_{2}+R_{1}R_{2}C_{1}s)(1+R_{2}C_{2}s)V_{C}(s)-(R_{1}+\mu R_{1}R_{2}C_{1}s)V_{C}(s)=R_{2}V_{1}(s)$$

$$(R_{1}+R_{2}+R_{1}R_{2}C_{1}s)(1+R_{2}C_{2}s)V_{C}(s)-(R_{1}V_{C}(s))-R_{1}R_{2}C_{1}s\mu V_{C}(s)=R_{2}V_{1}(s)$$

$$(R_{1}+R_{2}+R_{1}R_{2}C_{1}s)(1+R_{2}C_{2}s)=R_{1}+R_{1}R_{2}C_{2}s+R_{2}+R_{2}^{2}C_{2}s+R_{1}R_{2}C_{1}s+R_{1}R_{2}^{2}C_{1}C_{2}s^{2}$$

$$(R_{1}+R_{1}R_{2}C_{2}s+R_{2}+R_{2}^{2}C_{2}s+R_{1}R_{2}C_{1}s+R_{1}R_{2}^{2}C_{1}C_{2}s^{2}-R_{1}-R_{1}R_{2}C_{1}s\mu)V_{C}(s)=R_{2}V_{1}(s)$$

$$(R_{1}R_{2}C_{2}s+R_{2}+R_{2}^{2}C_{2}s+R_{1}R_{2}C_{1}s+R_{1}R_{2}^{2}C_{1}C_{2}s^{2}-R_{1}R_{2}C_{1}s\mu)V_{C}(s)=R_{2}V_{1}(s)$$

But here, I understand the way to go is using the fact of \$V_{2}(s)=\mu V_{C}(s)\$, but I got lost, how to group it to get the \$H(s)\$?

Answer 1

The fast analytical circuits techniques or FACTs described in my book on the subject offer a quick and convenient way to obtain the transfer function of this filter. However, it is important to note that the provided simplified schematic is wrong as the op-amp error voltage is wrongly taken across \$C_2\$. The correct equivalent circuit is shown below:

From there, you can apply the FACTs and start by analyzing the circuit for \$s=0\$ in which all caps are open. You obtain \$H_0\$ which is not the op-amp open-loop gain.

Then, you turn the excitation off - the input source is replaced by a short circuit - and you determine the resistance \$R\$ "seen" from the capacitors connecting terminals. The below picture shows the steps, some KVL and KCL are needed but this is pretty simple. And if you make a mistake, just solve the guilty sketch and straighten the all equation up without restarting from scratch:

There is no zero in this circuit because turning \$C_1\$ and \$C_2\$ in their high-frequency state (a short circuit) gives a 0-V output. Now assemble the time constants you have found and compare the response in phase and magnitude with a SIMetrix simulation:

The final transfer function appears in a clear and ordered manner - this is a low-entropy expression and it can be reworked to highlight salient characteristics such as the quality coefficient and the resonant frequency.

Answer 2

Here comes my recommendation for finding the transfer function of a Sallen-Key filter:

• Use only conductances y1....y4 for the passive components;

• Write down the two node equations for the two node voltages Vb and Vc (with finite and fixed closed-loop gain A for the amplifier);

• Solve for V2(s)/V1(s) and introduce y=1/R and y=sC.

Comment: When using conductances Y, the capacitors are considered from the beginning as sC - and, consequently, the transfer function has the classical standard form of a polynominal in "s".

Answer 3

The Sallen–Key circuit

^{simulate this circuit – Schematic created using CircuitLab}

\$V_c = V_o \cdot \frac{R_4}{R_f+R_4} = \frac{V_o}{K} \: \: \: \text{where} \: \: \: K = 1+ \frac{R_f}{R_4}\$

The node equations for A and B are

$$\begin{align*} \frac{V_a-V_\text{in}}{R_1} + \frac{V_a-V_b}{R_2} + (V_a-V_o)sC_1 = 0 \\ \\ \frac{V_b-V_a}{R_2} + V_bsC_2 = 0 \end{align*}$$

Because there is negative feedback \$V_b = V_c\$ (virtual short). Substituting this for \$V_b\$ and solving the two equations with respect to \$V_a\$ and \$V_o\$ you get

$$V_o = V_\text{in} \cdot \frac{K}{s^2 + s(\frac{1}{R_2C_2} + \frac{1-K}{R_2C_1} + \frac{1}{R_1C_2}) + \frac{1}{R_1R_2C_1C_2}} $$

P.S.: There isn't any extra reward for finding the transfer function of circuits by hand.

Answer 4

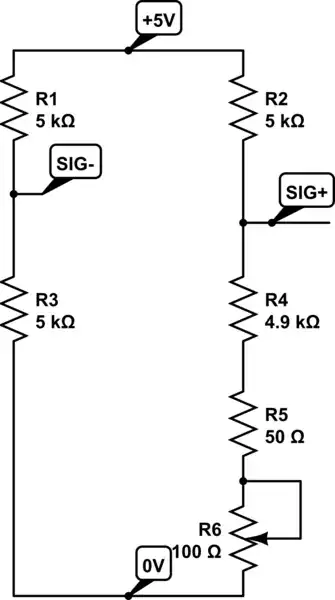
Well, we are trying to analyze the following circuit:

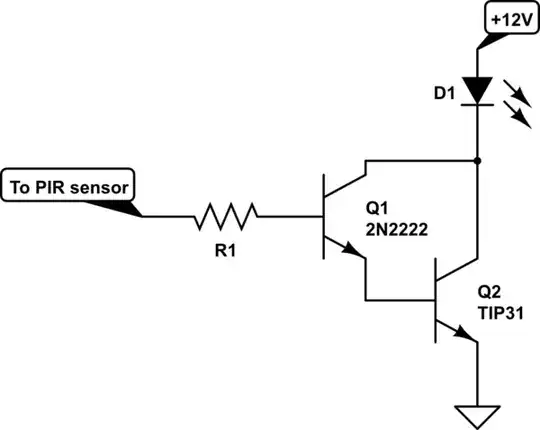
^{simulate this circuit – Schematic created using CircuitLab}

When we use and apply KCL, we can write the following set of equations:

$$ \begin{cases} \begin{alignat*}{1} \text{I}_1&=\text{I}_2+\text{I}_5\\ \\ \text{I}_2&=\text{I}_3+\text{I}_4\\ \\ 0&=\text{I}_0+\text{I}_4+\text{I}_5\\ \\ \text{I}_3&=\text{I}_0+\text{I}_1 \end{alignat*} \end{cases}\tag1 $$

When we use and apply Ohm's law, we can write the following set of equations:

$$ \begin{cases} \begin{alignat*}{1} \text{I}_1&=\frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1}\\ \\ \text{I}_2&=\frac{\text{V}_1-\text{V}_2}{\text{R}_2}\\ \\ \text{I}_3&=\frac{\text{V}_2}{\text{R}_3}\\ \\ \text{I}_4&=\frac{\text{V}_2-\text{V}_3}{\text{R}_4}\\ \\ \text{I}_5&=\frac{\text{V}_1-\text{V}_3}{\text{R}_5} \end{alignat*} \end{cases}\tag2 $$

We also notice that \$\text{V}_3=\text{n}\cdot\text{V}_2\$.

Substitute \$(2)\$ into \$(1)\$, in order to get:

$$ \begin{cases} \begin{alignat*}{1} \frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1}&=\frac{\text{V}_1-\text{V}_2}{\text{R}_2}+\frac{\text{V}_1-\text{V}_3}{\text{R}_5}\\ \\ \frac{\text{V}_1-\text{V}_2}{\text{R}_2}&=\frac{\text{V}_2}{\text{R}_3}+\frac{\text{V}_2-\text{V}_3}{\text{R}_4}\\ \\ 0&=\text{I}_0+\frac{\text{V}_2-\text{V}_3}{\text{R}_4}+\frac{\text{V}_1-\text{V}_3}{\text{R}_5}\\ \\ \frac{\text{V}_2}{\text{R}_3}&=\text{I}_0+\frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1} \end{alignat*} \end{cases}\tag3 $$

Now, we can solve the transfer function (with \$\text{R}_4\to\infty\$):

$$\mathcal{H}:=\frac{\text{V}_3}{\text{V}_\text{i}}=\frac{\text{n}\text{R}_3\text{R}_5}{\text{R}_1\left(\text{R}_2+\text{R}_5+\text{R}_3\left(1-\text{n}\right)\right)+\text{R}_5\left(\text{R}_2+\text{R}_3\right)}\tag4$$

Now, applying this to your circuit we need to use Laplace transform:

• $$\text{R}_3=\frac{1}{\text{sC}_1}\tag5$$
• $$\text{R}_5=\frac{1}{\text{sC}_2}\tag6$$

So, we get:

\begin{equation} \begin{split} \mathscr{H}\left(\text{s}\right)&=\frac{\displaystyle\text{n}\cdot\frac{1}{\text{sC}_1}\cdot\frac{1}{\text{sC}_2}}{\displaystyle\text{R}_1\left(\text{R}_2+\frac{1}{\text{sC}_2}+\frac{1}{\text{sC}_1}\cdot\left(1-\text{n}\right)\right)+\frac{1}{\text{sC}_2}\cdot\left(\text{R}_2+\frac{1}{\text{sC}_1}\right)}\\ \\ &=\frac{\text{n}}{\text{C}_1\text{C}_2\text{R}_1\text{R}_2\text{s}^2+\left(\text{C}_1\left(\text{R}_1+\text{R}_2\right)-\text{C}_2\text{R}_1\left(\text{n}-1\right)\right)\text{s}+1} \end{split}\tag7 \end{equation}

Now, when we want to find the bode-plot of this filter we can take a look at the modulus of \$(7)\$ with \$\text{s}=\text{j}\omega\$:

\begin{equation} \begin{split} \left|\underline{\mathscr{H}}\left(\text{j}\omega\right)\right|&=\left|\frac{\text{n}}{\text{C}_1\text{C}_2\text{R}_1\text{R}_2\left(\text{j}\omega\right)^2+\left(\text{C}_1\left(\text{R}_1+\text{R}_2\right)-\text{C}_2\text{R}_1\left(\text{n}-1\right)\right)\text{j}\omega+1}\right|\\ \\ &=\frac{\left|\text{n}\right|}{\left|\text{C}_1\text{C}_2\text{R}_1\text{R}_2\left(\text{j}\omega\right)^2+\left(\text{C}_1\left(\text{R}_1+\text{R}_2\right)-\text{C}_2\text{R}_1\left(\text{n}-1\right)\right)\text{j}\omega+1\right|}\\ \\ &=\frac{\left|\text{n}\right|}{\left|1-\text{C}_1\text{C}_2\text{R}_1\text{R}_2\omega^2+\left(\text{C}_1\left(\text{R}_1+\text{R}_2\right)-\text{C}_2\text{R}_1\left(\text{n}-1\right)\right)\omega\text{j}\right|}\\ \\ &=\frac{\left|\text{n}\right|}{\sqrt{\left(1-\text{C}_1\text{C}_2\text{R}_1\text{R}_2\omega^2\right)^2+\left(\left(\text{C}_1\left(\text{R}_1+\text{R}_2\right)-\text{C}_2\text{R}_1\left(\text{n}-1\right)\right)\omega\right)^2}} \end{split}\tag8 \end{equation}

And the argument is given by:

\begin{equation} \begin{split} \arg\left(\underline{\mathscr{H}}\left(\text{j}\omega\right)\right)&=\arg\left(\frac{\text{n}}{\text{C}_1\text{C}_2\text{R}_1\text{R}_2\left(\text{j}\omega\right)^2+\left(\text{C}_1\left(\text{R}_1+\text{R}_2\right)-\text{C}_2\text{R}_1\left(\text{n}-1\right)\right)\text{j}\omega+1}\right)\\ \\ &=\arg\left(\frac{\text{n}}{\underbrace{1-\text{C}_1\text{C}_2\text{R}_1\text{R}_2\omega^2}_{:=\space\alpha}+\underbrace{\left(\text{C}_1\left(\text{R}_1+\text{R}_2\right)-\text{C}_2\text{R}_1\left(\text{n}-1\right)\right)\omega}_{:=\space\beta}\cdot\text{j}}\right)\\ \\ &=\arg\left(\text{n}\right)-\arg\left(\alpha+\beta\text{j}\right)\\ \\ &=\begin{cases}0&\text{if}\space\text{n}\ge0\\\\\pi&\text{if}\space\text{n}<0\end{cases}-\begin{cases} 0&\text{if}\space\alpha\ge0\space\wedge\space\beta=0\\ \\ \pi&\text{if}\space\alpha<0\space\wedge\space\beta=0\\ \\ \arctan\left(\frac{\beta}{\alpha}\right)&\text{if}\space\alpha>0\space\wedge\space\beta>0\\ \\ \frac{\pi}{2}+\arctan\left(\frac{\left|\alpha\right|}{\beta}\right)&\text{if}\space\alpha<0\space\wedge\space\beta>0\\ \\ \frac{3\pi}{2}+\arctan\left(\frac{\alpha}{\left|\beta\right|}\right)&\text{if}\space\alpha>0\space\wedge\space\beta<0 \end{cases} \end{split}\tag9 \end{equation}

Just for the sake of it, let's assume \$\text{R}_1=\text{R}_2:=\text{R}\$ and \$\text{C}_1=\text{C}_2:=\text{C}\$, than we find:

$$\left|\underline{\mathscr{H}}\left(\text{j}\omega\right)\right|=\frac{\left|\text{n}\right|}{\sqrt{\left(1-\left(\text{CR}\omega\right)^2\right)^2+\left(\text{CR}\omega\left(3-\text{n}\right)\right)^2}}\tag{10}$$

---

I used the following Mathematica-code, to solve for \$(7)\$:

In[1]:=Clear["Global`*"];
R3 = 1/(s*C1);
R5 = 1/(s*C2);
R4 = Infinity;
FullSimplify[(V3 /. 
    Solve[{I1 == I2 + I5, I2 == I2 == I3 + I4, 0 == I0 + I4 + I5, 
       I3 == I0 + I1, I1 == (Vi - V1)/R1, I2 == (V1 - V2)/R2, 
       I3 == V2/R3, I4 == (V2 - V3)/R4, I5 == (V1 - V3)/R5, 
       V3 == n*V2}, {I0, I1, I2, I3, I4, I5, V1, V2, V3}][[1]])/Vi]

Out[1]=n/(1 - C2 (-1 + n) R1 s + C1 s (R1 + R2 + C2 R1 R2 s))