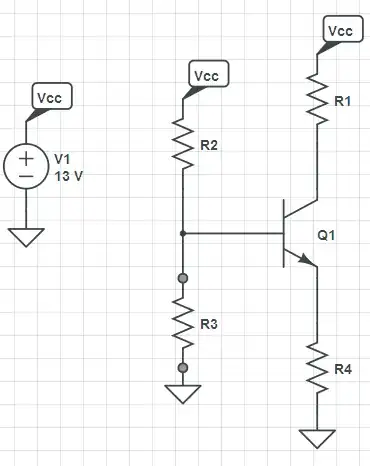
I'm to the task to design a BJT Common-Emitter Amplifier with resistance at the emitter as in the figure, and for that I need to:
- get the values for \$R_{1}\$, \$R_{2}\$, \$R_{C}\$ and \$R_{E}\$
- given \$I_{CQ} = 3\text{mA}\$ , \$V_{CEQ} = 6.5\text{V}\$ ,\$V_{CC}=13\text{V}\$ and \$\beta = 380\$ for a BC547C transistor.
Currently I'm able to analyze correctly the circuit given the resistances, but the reverse process, that is, getting the resistances values given only the operating point is what is giving me problems as there is various "rules of thumb" and considerations to make, I'm trying to use the "1/3 rule of thumb" (\$V_{E} = V_{C} = V_{CE}= V_{CC}/3\$) but I'm not getting the expected results \$V_{CE}\$ since \$V_{CE}\$ is already given.
How can I go to design this circuit?