1

I'm tasked with making a 4-7 decoder for a 7-segment LED (common anode).

I am an extreme layman (1st year EEE student)

I have 4 inputs (A,B,C,D)

A inputs are: 0000000011111111
B inputs are: 0000111100001111
C inputs are: 0011001100110011
D inputs are: 0101010101010101

'a', 'b', 'c', 'd', 'e', 'f', 'g' are the segments.

Take segment 'd' for example.

enter image description here

I got AC' + A'B'D' + B'CD + BCD' + BC'D

Would I have 5 AND gates going into a 5-input OR gate?

I think I'm slowly getting the hang of it - but I have nobody to verify if it's correct so I can proceed.

My big confusion is as I need to use common anode, I need to look for the '0's on the K-map and not the '1's, correct?

JYelton
  • 32,302
  • 33
  • 134
  • 249
NonComposMentis
  • 25
  • 2
  • You should be able to verify this yourself by creating a truth table for the reduced logic equation that you produced. Make sure that its result is 1 only when you want it to be 1 and is 0 only when you want it to be 0. – Elliot Alderson Dec 19 '22 at 13:29
  • Depends. Back in the 7400 days, funny-bones insisted in throwing in EXOR gates. And AND gates you need no more than four?! – greybeard Dec 19 '22 at 18:38

1 Answers1

0

I'm tasked with making a 4-7 decoder for a 7-segment LED (common anode).

You can also implement the logic table with multiplexers directly: set their inputs with the desired output values. This is definitely simpler and often faster, too, than and-or gates. Especially for early CMOS logic (mid-late 70s): the 8-1 mux propagates in about the same time as a 4-input gate (say CD4512).

For example:

schematic

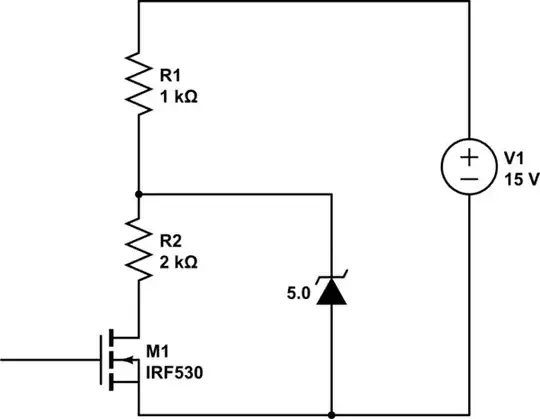
simulate this circuit – Schematic created using CircuitLab

We of course don't need two multiplexers: one will do.

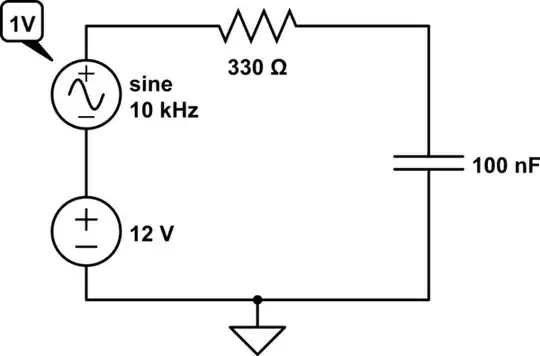
schematic

simulate this circuit

So, a 7-segment decoder with multiplexers is essentially 7xCD4512 + 1xCD4069, or their 74xx equivalents.

That's how modern logic is implemented anyway: the LUTs inside of FPGAs, for example. It is somewhat awkward that we often start with a truth table, translate it into equations in VHDL or Verilog, and that gets translated back into a truth table that's then provided as an input to a MUX. For wide-output LUTs, several parallel MUXes share a decoder/driver section to minimize die area.

On a digital ASIC, it's not unusual to have all combinatorial functions use LUT cells (fixed-input MUXes). Any n-input function is the same layout, with different metallization to select 1s and 0s going to the inputs.

Putting combinatorial logic together out of actual gates is mostly a retro-electronics and retrocomputing adventure at this point. Even if you're doing discrete stuff, for anything that can't be solved with one or two gates, or a matching combinatorial function (decoders, for example), a LUT wins every time. And that applied even in the 70s - a lot of glue combinatorial logic could have used MUXes instead. And it's not a recent discovery, of course: this approach was widely taught, and was publicized in popular design books, such as those by Don Lancaster (TTL Cookbook, CMOS Cookbok published in mid-70s!).

There is a certain tendency to teach slightly useless concepts in engineering, and Karnaugh maps aren't very useful whether you design discrete logic or VLSI...

Kuba hasn't forgotten Monica
  • 32,734
  • 1
  • 38
  • 103