Why can we deduce certain voltages from the op-amp?

Question

I am learning about ideal op-amps. One of the main characteristics of this device is the infinite open loop gain, which means that we can deduce that the 2 input voltages are the same as \$v_2-v_1=\frac{v_3}{A} =0\$ because the gain is ideally infinite.

This is a deduction we can make because we also assume the op amp is generating a finite output signal, but why can we assume this?

It seems like we are making a backwards deduction, as in we know the gain is infinite, and thus the deduction is the output signal is also infinite, but if the output signal is finite the only reason this can be is because the two input voltages are the same, however this deduction is based on the assumption that the output signal is finite.

Why can we assume this? In real life, the open loop gain will be very large but not infinite. Why can we assume the output signal will be a "normal" signal and not massively amplified?

Answer 1

It looks like you confused open-loop operation with closed-loop operation.

---

It's true that the voltage difference of the inputs are multiplied by infinity. And theoretically, an op amp should generate infinite voltage when running in open-loop:

$$v_2-v_1=\frac{v_3}{A}$$

However, the equation you wrote

$$v_2-v_1=\frac{v_3}{A}=0$$

is wrong. Because,

• We assume the two input voltages to be equal if and only if there's a feedback. Because the op amp circuit turns into a stabilisation circuit that tries to equalise its both inputs. Stabilisation happens when there's a feedback.
• We can't include the open-loop gain into this equation because feedback basically dominates the closed-loop (overall) gain.

---

Now, don't take "infinity" in the op amp's open-loop gain definition as \$\infty\$ because basically what it means is an "unknown, large enough, finite number" to make some simplifications easier.

From basic feedback theory, the gain of an open loop system decreases by the feedback. Below is a representation of negative feedback:

^{Img Src: Analog Semi article}

The gain with feedback is

$$ G=\frac{A}{\beta A + 1}\approx\frac{1}{\beta} $$

If \$A\$ was not large enough then the term \$\beta A\$ wouldn't be large enough therefore we wouldn't be able to get rid of \$+1\$ term.

Plus, if \$A\$ was \$\infty\$ we wouldn't be able to get rid of it to make the gain equation \$A\$-independent as \$\infty\$ on both numerator and denominator can't be cancelled. We want the gain to be independent from \$A\$ because it is way too large to be a useful number considering the numbers/levels for the input we will be dealing with.

---

In real life, the open loop gain will be very large but not infinite, why can we assume the output signal will be a "normal" signal and not massively amplified?

Because almost all of the op amp circuits in real life have feedback therefore the gain is way lower than the open-loop gain. A numerical example: An op amp's open-loop gain can be 1x10⁸ but in real life it's going to be in closed-loop operation therefore the overall gain can be 200 which cannot be compared to the open-loop gain. This amount of gain allows the output to be "normal" (assuming you meant "unclipped").

Answer 2

we also assume the op amp is generating a finite output signal, but why can we assume this?

We assume this because, in the real world, op-amp output voltages are limited to a range that's within the voltage power rails AND, when we want a linear amplifier using negative feedback, we want a finite output voltage.

Why can we assume the output signal will be a "normal" signal and not massively amplified?

You are getting things back to front; putting the cart before the horses so to speak. The op-amp output IS finite therefore the voltage difference between the inputs (when negative feedback is used) is zero for an infinite gain theoretical op-amp.

Answer 3

dismantling some of your writing

You've already got some useful answers. And I certainly don't intend on muddling things further. I just have a slightly different slant to offer.

Let's start here:

I am learning about ideal op-amps. One of the main characteristics of this device is the infinite open loop gain, which means that we can deduce that the 2 input voltages are the same as v2−v1=v3A=0 because the gain is ideally infinite.

There's an assumption buried in the above that I want to haul out into plain view. Perhaps the best way to do that is to just draw this ideal opamp:

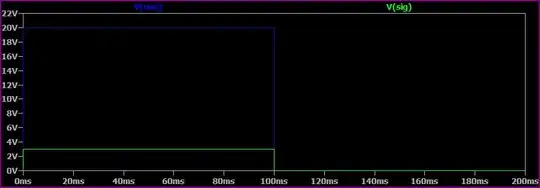
^{simulate this circuit – Schematic created using CircuitLab}

There's nothing there to cause \$V_{( - )}=V_{( + )}\$. They are independent of each other at this point. We could set \$V_{( - )}=+2\:\text{V}\$ and \$V_{( + )}=-1\:\text{V}\$. That may leave us with a bit of an difficult situation considering \$V_{_\text{OUT}}\$ as it implies multiplying a finite difference by infinity. But that detail doesn't force the two inputs to be the same.

The point to make here is that it is only with the addition of feedback from the output that we can arrange things so that \$V_{( - )}=V_{( + )}\$. So there was something implied in your writing -- feedback -- that you may or may not have been thinking about when writing. I just want to make sure to call it out to your attention so that it doesn't slip under some rug.

This is a deduction we can make because we also assume the op amp is generating a finite output signal, but why can we assume this?

When premises are false, even valid logic cannot rescue the conclusion. So This is just wrong. We don't assume the inputs are the same. In fact, it would be very easy for me to show you a circuit where the opamp is nearly ideal and yet the inputs are different by more than a few volts. This can be due to a design error but it is also fairly common in good designs where the device is operated as a comparator. So, no. We don't assume it. We prove it, when appropriate, as an output result taken from true axioms and valid logic leading to soundly reasoned conclusions.

It seems like we are making a backwards deduction, as in we know the gain is infinite, and thus the deduction is the output signal is also infinite, but if the output signal is finite the only reason this can be is because the two input voltages are the same, however this deduction is based on the assumption that the output signal is finite.

Why can we assume this? In real life, the open loop gain will be very large but not infinite. Why can we assume the output signal will be a "normal" signal and not massively amplified?

So, by now, you've gone down the rabbit hole because you started with some incorrect assumptions. Given those, I can see why you imagine some kind of circular logic. But that's definitely not the case.

inside a bipolar (BJT) opamp

Before finishing up by solving for an analog amplifier stage with voltage gain, I'd like to take a quick break from the above. Kind of an intermission of sorts.

Let's take a moment and just observe something about the input stage that's inside a bipolar (BJT) opamp. It's usually related to what may be called a differential pair of BJTs. Without belaboring the details, the idea is that the emitters of the two BJTs are tied together and given a kite tail of sorts which is an ideal (hypothetically, but not really) current source/sink. (Together, the two BJTs plus the 'kite tail' current source/sink is called a long-tailed pair.) If the bases of the two BJTs are exactly equal, then their collectors will exactly split that current in half, each taking up \$\frac12\$ of the tail current. But if there's so much as a slight difference, then more of the current will go one direction than the other. It's kind of like a water valve which can split the flow of water into two different hoses/pipes, but where you can control the diversion.

As it turns out, this only works within a small difference range. If the voltage difference (BJT input opamp) exceeds \$200\:\text{mV}\$ then the entire flow is directed one way and not the other. And any further difference isn't going to change anything. In effect, the ability to continue applying some hypothetical voltage gain has been destroyed.

So real opamps have a narrow range within which their input differences are multiplied (approximately) by some assumed, fixed voltage gain. And it is a pretty narrow range. So a good design (excepting comparators, for example) will arrange things so that both inputs are arbitrarily close, but not exactly the same.

You need to keep this also in mind. (Also, opamps will often protect their inputs so that the difference cannot be too excessive, by just internally dumping current and loading down your source a lot when you exceed some small range of allowed difference. Diode protection is one way to do this.)

Now we can look at an analog amplifier stage with voltage gain.

opamp with feedback and finite voltage gain

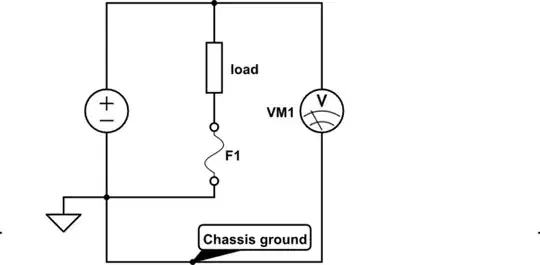
^{simulate this circuit}

Here, we want to assume that both inputs are identical. And since we know \$V_{( + )}=0\:\text{V}\$, then that means \$V_{( - )}=0\:\text{V}\$. But how do we know that? Well, we don't because it's not really true. We just know that the difference will probably be very small.

But you need to work through that, rather than assume it. So let's not assume it. Let's prove it.

As \$V_{_\text{OUT}}=A\cdot\left(V_{( + )}-V_{( - )}\right)\$ and \$V_{( + )}=0\:\text{V}\$ then \$V_{_\text{OUT}}=-A\cdot V_{( - )}\$. But this output drives one side of a resistor divider with the other end at \$V_{_\text{IN}}\$. So the midpoint of the divider will be \$V_{( - )}=\frac{V_{_\text{IN}}\cdot R_{_\text{F}} + V_{_\text{OUT}}\cdot R_{_\text{IN}}}{R_{_\text{IN}}+R_{_\text{F}}}\$.

As we already know that \$V_{( - )}=-\frac{V_{_\text{OUT}}}{A}\$, find \$V_{_\text{OUT}}=-V_{_\text{IN}}\cdot\left[\frac1{\left(1+\frac1{A}\right)\cdot \frac{R_{_\text{IN}}}{R_{_\text{F}}}+\frac1{A}}\right]=-A\cdot V_{( - )}\$.

Or, that \$V_{( - )}=-\frac{V_{_\text{IN}}}{A}\cdot\left[\frac1{\left(1+\frac1{A}\right)\cdot \frac{R_{_\text{IN}}}{R_{_\text{F}}}+\frac1{A}}\right]\$.

Now, pause for a moment.

You should be able to see easily now that as \$A\to\infty\$ then \$V_{( - )}\to 0\:\text{V}\$ and \$V_{_\text{OUT}}\to -V_{_\text{IN}}\cdot\frac{R_{_\text{F}}}{R_{_\text{IN}}}\$.

So it's not assumed. If you are willing to take \$A\to\infty\$ then it is proved.

(Note that it is proved only assuming the circuit I provided, which has feedback from the output backwards to one of the inputs. If that wasn't present, then the results would of course be different.)

If you are a designer using practical opamps then you will be aware that \$A\ne\infty\$ and then of course there will be a small difference between the inputs. But this fact that the difference is small is as a result of feedback in this particular schematic, which allows the extremely high open loop opamp voltage gain to operate on the inputs.

You are, in fact, encouraged to use any particular value for \$A\$ to see where that takes you in this case. Try out 10, 100, 1000, etc. See what happens. It's useful to go through the exercise.

Answer 4

An ideal op amp has infinite gain which means that theoretically its output will go to infinity with almost zero difference between its inputs.

A real op amp will have a very large gain (but not infinite). This is what we refer to as the open loop gain. So a real op amp will have a finite output when there is a finite difference voltage between its inputs.

For a real op amp Vout = (V+ - V-)*Aol where Aol is the op amp's open loop gain.

A raw op amp operating in open loop is, in the majority of cases, pretty useless to us and we must add some negative feedback around the op amp (usually a couple of resistors) to tame that huge open loop gain and force the overall amplifier to have a much lower and more useful closed loop gain.

So, we could add a 10k input resistor and 100k feedback resistor to an op-amp configured as an inverting amplifier to achieve a more useful dc closed loop gain of Vout/Vin = -10. This is the gain of the overall amplifier.

But it's important to realise that by operating the op-amp in a closed loop configuration with a closed loop gain of -10, we have not actually reduced the op amp's open loop gain and the op amp is still operating with its very high open loop gain forcing the actual inputs to have a difference voltage between them equal to Vout/Aol. With a typical output of a few volts and a very large open loop gain it means that the difference voltage between the inputs will be very small.

As frequency is increased the op amp's open loop gain reduces and so, in a closed loop configuration, as frequency increases the difference voltage between the inputs increases in an attempt to prevent the output voltage from reducing (too much).

Answer 5

I'll attempt to make the shortest answer, which may also be helpful:

We can assume it because we design circuits that are balanced with a finite output voltage. Not only finite, but within the power supply rails, and also within the smaller output swing of the amplifier).

If the circuit cannot balance with a finite output voltage (say, a comparator with hysteresis or an amplifier clipping because the output is saturated) we don't use that approximation (it is not useful), and use some other method of analysis.

If you don't fully understand the circuit and analysis using those assumptions leads to an impossible output voltage or an unstable balance point, then that's a sign that another approach is required.

Answer 6

For an ideal op-amp, without feedback, your concerns are valid. Any non-zero difference between inverting and non-inverting input potentials results in an infinite output. The resulting gain equation for an open-loop ideal op-amp is algebraically dubious.

Even when we employ negative feedback, the resulting algebra contains an infinity in a numerator somewhere:

^{simulate this circuit – Schematic created using CircuitLab}

Bear with me here. The inverting input is presented with some fraction β of the output potential at X, giving us these equations:

$$ \begin{aligned} V_X &= A(V_P - V_Q) \\ \\ V_Q &= \beta V_X \end{aligned} $$

These simultaneous equations are whittled down to a single equation relating \$V_P\$ and \$V_X\$:

$$ \begin{aligned} V_X &= A(V_P - \beta V_X) \\ \\ &= AV_P - A\beta V_X \\ \\ V_X + A\beta V_X &= AV_P \\ \\ V_X ( 1 + A\beta) &= A V_P \\ \\ V_X &= V_P\left(\frac{A}{1+A\beta}\right) \end{aligned} $$

At this point the typical engineer is happy to continue, safe in the knowledge that both '\$A\$'s are the same '\$A\$' and derive the famous closed-loop gain equation. Dividing top and bottom by \$A\$:

$$ \begin{aligned} V_X &= V_P \left(\frac{1}{\frac{1}{A}+\beta}\right) \\ \\ &= V_P \left(\frac{1}{0+\beta}\right) \\ \\ &= \frac{V_P}{\beta} \end{aligned} $$

However, the mathematician looking over the engineer's shoulder as he does this manipulation is screaming bloody murder. He scoffs, for the same reason you have raised, at this is reckless treatment of infinities. He says "this last equation is true for every value of \$A\$ except the case \$A=\infty\$! You assume there is such a thing as two identical infinities!"

Then he corrects the engineer:

$$ \begin{aligned} V_X &\rightarrow \lim_{A\rightarrow \infty}V_P\left(\frac{A}{1+A\beta}\right) \\ \\ &\rightarrow \frac{V_P}{\beta} \end{aligned} $$

which states that for very large values of \$A\$, \$V_X\$ is very close indeed to \$\frac{V_P}{\beta}\$, but never forget that the relationship is just a very good approximation:

$$ \begin{aligned} V_X &\approx \frac{V_P}{\beta} \end{aligned} $$

In the real world, there are no ideal operational amplifiers, no such thing as infinities, and the best we can do (which is good enough) is produce op-amps with extremely high gain. It is not necessary to show algebraically what would happen if \$A = \infty\$, only what happens when \$A\$ is huge.

In other words, you are right to question the validity of the gain equation for the ideal op-amp, just as the mathematician did, and I applaud your criticism of it.