Transfer function with current source

Question

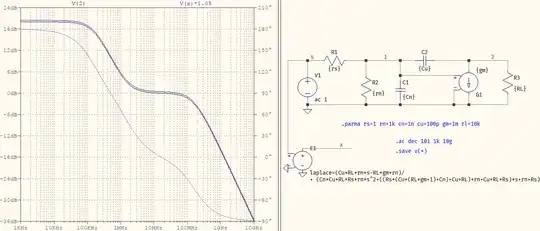
I have been trying this exercise for a while and I can't solve it.

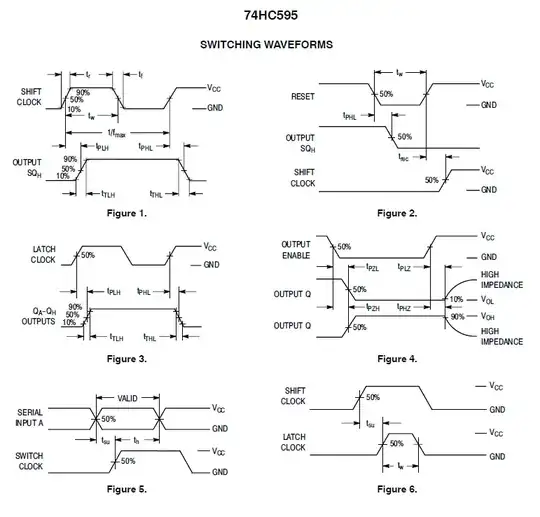
What they ask me to find is $$\frac{V_2\left(s\right)}{V_s\left(s\right)}=?$$

My best attempt has been the following

\begin{array}{l}\left[1\right]\ V_s\left(s\right)=R_sI1_{\left(s\right)}+Z\left(I1_{\left(s\right)}-I2_{\left(s\right)}\right)\\ \left[2\right]\ g_m=I2_{\left(s\right)}-I3_{\left(s\right)}\\ \left[3\right]\ \frac{I2_{\left(s\right)}}{sC_{\mu }}+R_LI3_{\left(s\right)}+Z\left(I2_{\left(s\right)}-I1_{\left(s\right)}\right)=0\\ \frac{I2_{\left(s\right)}}{sC_{\mu }}+R_LI3_{\left(s\right)}=Z\left(I1_{\left(s\right)}-I2_{\left(s\right)}\right)\\ \left[2\right]\ g_m+I3_{\left(s\right)}=I2_{\left(s\right)}\\ Rem\\ \left[1\right]\ V_s\left(s\right)=R_sI1_{\left(s\right)}+\frac{g_m+I3_{\left(s\right)}}{sC_{\mu }}+R_LI3_{\left(s\right)}\\ \frac{\ V_s\left(s\right)}{I3_{\left(s\right)}}=\frac{R_sI1_{\left(s\right)}}{I3_{\left(s\right)}}+\frac{g_m}{sC_{\mu }I3_{\left(s\right)}}+\frac{1}{sC_{\mu }}+R_L\\ \left[\frac{\ V_s\left(s\right)}{I3_{\left(s\right)}}=\frac{sC_{\mu }R_sI1_{\left(s\right)}+g_m+I3_{\left(s\right)}\left(1+sC_{\mu }R_L\right)}{sC_{\mu }I3_{\left(s\right)}}\right]\\ \left[2\right]\ I2_{\left(s\right)}-g_m=I3_{\left(s\right)}\\ \frac{\ V_s\left(s\right)}{I3_{\left(s\right)}}=\frac{sC_{\mu }R_sI1_{\left(s\right)}+g_m+\left(I2_{\left(s\right)}-g_m\right)\left(1+sC_{\mu }R_L\right)}{sC_{\mu }\left(I2_{\left(s\right)}-g_m\right)}\\ \left[3\right]\ \frac{I2_{\left(s\right)}}{sC_{\mu }}+R_LI3_{\left(s\right)}=ZI1_{\left(s\right)}-ZI2_{\left(s\right)}\\ \frac{I2_{\left(s\right)}}{ZsC_{\mu }}+\frac{R_LI3_{\left(s\right)}}{Z}+I2_{\left(s\right)}=I1_{\left(s\right)}\end{array}

After getting there I don't know what to do

[Update]

I was able to solve it now, thanks to everyone who replied and showed me so many methods.

What I did was transform the voltage source, then apply a divider and get the equation through nodes.

So I got the following equations

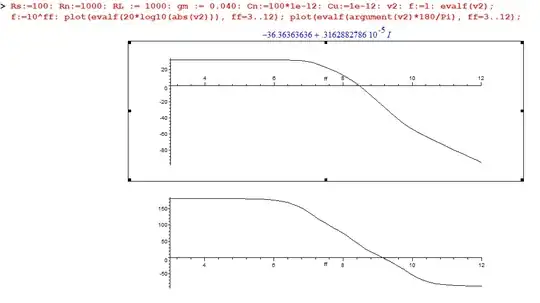
$$\begin{array}{l}\sum _{ }^{ }i_e\left(t\right)=\sum _{ }^{ }i_s\left(t\right)\\ \left[1\right]\ \frac{V_s\left(s\right)}{R_s}=g_tV_t\left(s\right)+sC_{\eta }V_t\left(s\right)+sC_{\mu }\left(V_t\left(s\right)-V_2\left(s\right)\right)\\ \left[2\right]\ sC_{\mu }\left(V_t\left(s\right)-V_2\left(s\right)\right)=g_m\cdot V_t\left(s\right)+\frac{V_2\left(s\right)}{R_L}\\ \ sC_{\mu }V_t\left(s\right)-sC_{\mu }V_2\left(s\right)-g_m\cdot V_t\left(s\right)=\frac{V_2\left(s\right)}{R_L}\\ \ V_t\left(s\right)\left(sC_{\mu }-g_m\right)=\left(\frac{1}{R_L}+sC_{\mu }\right)V_2\left(s\right)\\ V_t\left(s\right)\left(sC_{\mu }-g_m\right)=\left(\frac{1+R_LsC_{\mu }}{R_L}\right)V_2\left(s\right)\\ V_t\left(s\right)=V_2\left(s\right)\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)\\ Sus\ 1\\ \frac{V_s\left(s\right)}{R_s}=g_tV_t\left(s\right)+sC_{\eta }V_t\left(s\right)+sC_{\mu }\left(V_t\left(s\right)-V_2\left(s\right)\right)\\ \frac{V_s\left(s\right)}{R_s}=g_tV_2\left(s\right)\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+sC_{\eta }V_2\left(s\right)\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+sC_{\mu }\left(V_t\left(s\right)-V_2\left(s\right)\right)\\ \frac{V_s\left(s\right)}{R_s}=g_tV_2\left(s\right)\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+sC_{\eta }V_2\left(s\right)\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+g_m\cdot V_2\left(s\right)\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+\frac{V_2\left(s\right)}{R_L}\\ \frac{V_s\left(s\right)}{R_sV_2\left(s\right)}=g_t\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+sC_{\eta }\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+g_m\left(\frac{1+R_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}\right)+\frac{1}{R_L}\\ \frac{V_s\left(s\right)}{R_sV_2\left(s\right)}=\frac{g_t+g_tR_LsC_{\mu }}{R_L\left(sC_{\mu }-g_m\right)}+\frac{sC_{\eta }+s^2C_{\eta }C_{\mu }R_L}{R_L\left(sC_{\mu }-g_m\right)}+\frac{g_m+g_msC_{\mu }R_L}{R_L\left(sC_{\mu }-g_m\right)}+\frac{sC_{\mu }-g_m}{R_L\left(sC_{\mu }-g_m\right)}\\ \frac{V_s\left(s\right)}{R_sV_2\left(s\right)}=\frac{g_t+g_tR_LsC_{\mu }+sC_{\eta }+s^2C_{\eta }C_{\mu }R_L+g_m+g_msC_{\mu }R_L+sC_{\mu }-g_m}{R_L\left(sC_{\mu }-g_m\right)}\\ \frac{V_s\left(s\right)}{R_sV_2\left(s\right)}=\frac{s^2C_{\eta }C_{\mu }R_L+s\left(C_{\eta }+C_{\mu }+g_tR_LC_{\mu }+g_mC_{\mu }R_L\right)+g_t}{R_L\left(sC_{\mu }-g_m\right)}\\ \frac{R_sV_2\left(s\right)}{V_s\left(s\right)}=\frac{R_L\left(sC_{\mu }-g_m\right)}{s^2C_{\eta }C_{\mu }R_L+s\left(C_{\eta }+C_{\mu }+g_tR_LC_{\mu }+g_mC_{\mu }R_L\right)+g_t}\\ \left[\frac{V_2\left(s\right)}{V_s\left(s\right)}=\frac{sC_{\mu }-g_m}{s^2C_{\eta }C_{\mu }R_L+s\left(C_{\eta }+C_{\mu }+g_tR_LC_{\mu }+g_mC_{\mu }R_L\right)+g_t}\cdot \frac{R_L}{R_s}\right]\\ where\ g_t\ =\frac{1}{R_s}+\frac{1}{r_n}\end{array}$$

Thank you all for responding

Answer 1

I don't know where you got that exercise but it is not an easy one. I have used the fast analytical circuits techniques (FACTs) described in my book on the subject. You first start by determining the dc gain and the time constants of the circuit:

You do the same for the zeroes realizing that only the series capacitor provides one. Assemble all the time constants together as in the below picture:

To check this expression, I have simulated the circuit in SIMetrix and imported the data in Mathcad. As you can see below, a perfect match:

Answer 2

As pointed out by @Verbal Kint, it is not an easy circuit (because of the two capacitors).

Here is a Maple sheet for this, the values chosen are of a "common" BJT EC configuration.

As "usual", I did the same thing with a simulator (did not check all yet).
Made with microcap v12.

Answer 3

If you have access to and can use a symbolic solver (or even a numerical one) then you can use the voltages, since it's ony two nodes. For example, in the picture below, using the annotated node labes, you can use Python to solve it:

import sympy as sp
sp.var('s')
sp.var('v1 v2 vs')
sp.var('Rs rn Cu Cn gm RL')
eq1=sp.Eq(v1*(1/Rs+1/rn+s*Cn+s*Cu), vs/Rs+v2*s*Cu)
eq2=sp.Eq(v2*(s*Cu+1/RL)+v1*gm, v1*s*Cu)
sp.solve([eq1, eq2],[v1, v2])

{v1: (Cu*RL*rn*s*vs + rn*vs)/(Cn*Cu*RL*Rs*rn*s**2 + Cn*Rs*rn*s + Cu*RL*Rs*gm*rn*s + Cu*RL*Rs*s + Cu*RL*rn*s + Cu*Rs*rn*s + Rs + rn), v2: (Cu*RL*rn*s*vs - RL*gm*rn*vs)/(Cn*Cu*RL*Rs*rn*s**2 + Cn*Rs*rn*s + Cu*RL*Rs*gm*rn*s + Cu*RL*Rs*s + Cu*RL*rn*s + Cu*Rs*rn*s + Rs + rn)}

(I see there are two answers now, I'll finish this since it involves Kirchhoff, which is what you tried, but the other way)

The test is easy enough:

I've shifted V(x) a bit otherwise they would completely overlap, just like the phase plots (i.e. the Laplace expression and the circuit are identical).

---

[edit]

If you have problems deciphering the code, here are the MathJax equations:

$$\begin{cases} V_1\left(\dfrac{1}{R_S}+\dfrac{1}{r_n}+sC_{\eta}+sC_{\mu}\right)&=\dfrac{V_S}{R_S}+V_2sC_{\mu} \\ V_2\left(sC_{\mu}+\dfrac{1}{R_L}\right)+g_mV_1&=V_1sC_{\mu} \end{cases} \tag{1}$$

There are two solutions, out of which the second one is of interest:

$$ \dfrac{V_2}{V_S}=-\dfrac{r_nR_LC_{\mu}s-g_mr_nR_L}{r_nR_LR_SC_{\eta}C_{\mu}s^2+\Biggr(\biggr(R_S\big(C_{\mu}(g_mR_L+1)+C_{\eta}\big)+R_LC{\mu}\biggr)r_n+R_LR_SC_{\mu}\Biggr)s+r_n+R_S} \tag{2} $$

---

[edit 2]

For the sake of completeness, here's the system of equations that can take you to solve the problem using your approach:

$$\begin{cases} 1&=R_Si_1+(i_1-i_2)r_n \\ (i_1-i_2)r_n&=\dfrac{i_2-i_3}{sC_{\eta}} \\ \dfrac{i_2-i_3}{sC_{\eta}}&=\dfrac{i_3}{sC_{\mu}}+g_m(i_1-i_2)r_n+R_Li_4 \\ i_3&=g_m(i_1-i_2)r_n+i_4 \end{cases} \tag{3}$$

There will be 4 solutions for \$i_{1,2,3,4}\$, out of which you need the 4th, multiplied with \$R_L\$, to give the output voltage: \$R_Li_4\$. The solution is (2), without the \$R_L\$ in the numerator. The code will have the same variables, declared with sp.var(), except the variables will be the 4 currents:

sp.var('s')
sp.var('Rs rn Cu Cn gm RL')
sp.var('i1 i2 i3 i4')
eq1=sp.Eq(1, Rs*i1+(i1-i2)*rn)
eq2=sp.Eq((i1-i2)*rn, (i2-i3)/s/Cn)
eq3=sp.Eq((i2-i3)/s/Cn, i3/s/Cu+gm*(i1-i2)*rn+RL*i4)
eq4=sp.Eq(i3, gm*(i1-i2)*rn+i4)
sp.solve([eq1, eq2, eq3, eq4], [i1, i2, i3, i4])

{i1: (Cn*Cu*RL*rn*s**2 + Cn*rn*s + Cu*RL*gm*rn*s + Cu*RL*s - Cu*gm*rn*s + Cu*rn*s + 1)/(Cn*Cu*RL*Rs*rn*s**2 + Cn*Rs*rn*s + Cu*RL*Rs*gm*rn*s + Cu*RL*Rs*s + Cu*RL*rn*s - Cu*Rs*gm*rn*s + Cu*Rs*rn*s + Rs + rn), i2: (Cn*Cu*RL*rn*s**2 + Cn*rn*s + Cu*RL*gm*rn*s - Cu*gm*rn*s + Cu*rn*s)/(Cn*Cu*RL*Rs*rn*s**2 + Cn*Rs*rn*s + Cu*RL*Rs*gm*rn*s + Cu*RL*Rs*s + Cu*RL*rn*s - Cu*Rs*gm*rn*s + Cu*Rs*rn*s + Rs + rn), i3: (Cu*RL*gm*rn*s - Cu*gm*rn*s + Cu*rn*s)/(Cn*Cu*RL*Rs*rn*s**2 + Cn*Rs*rn*s + Cu*RL*Rs*gm*rn*s + Cu*RL*Rs*s + Cu*RL*rn*s - Cu*Rs*gm*rn*s + Cu*Rs*rn*s + Rs + rn), i4: (-Cu*gm*rn*s + Cu*rn*s - gm*rn)/(Cn*Cu*RL*Rs*rn*s**2 + Cn*Rs*rn*s + Cu*RL*Rs*gm*rn*s + Cu*RL*Rs*s + Cu*RL*rn*s - Cu*Rs*gm*rn*s + Cu*Rs*rn*s + Rs + rn)}

Answer 4

For solving thease kinds of problems, I like to use lcapy a symbolic circuit analysis tool.

Numbering the upper nodes 1, 2, 3 from left to right, and noting the input and output voltages as ports we can represent the circuit as:

from lcapy import Circuit

cir = Circuit("""
Ps 1 0
Rs 1 2
Rn 2 0
Cn 2 0
Cu 2 3
Rl 3 0
Gm 3 0 2 0
P2 3 0
""")

print(cir.transfer("Ps", "P2"))
# Prints:

$$ \frac{\frac{1}{C_{n}} \frac{1}{C_{u}} \frac{1}{R_{s}} \left(C_{u} s + G_{m}\right)}{s^{2} + \frac{s \left(C_{n} R_{n} R_{s} - C_{u} G_{m} R_{l} R_{n} R_{s} + C_{u} R_{l} R_{n} + C_{u} R_{l} R_{s} + C_{u} R_{n} R_{s}\right)}{C_{n} C_{u} R_{l} R_{n} R_{s}} + \frac{R_{n} + R_{s}}{C_{n} C_{u} R_{l} R_{n} R_{s}}} $$

Answer 5

It's straightforward to apply KCL to the nodes on either side of \$C_\mu\$ and obtain two equations in two unknowns \$V_1\$ and \$V_2\$.

$$ \frac{V_s-V_1}{R_s}=\frac{V_1}{r_n}+\frac{V_1}{\frac{1}{s C_{\eta }}} +\frac{V_1-V_2}{\frac{1}{s C_{\mu }}}$$ $$\frac{V_1-V_2}{\frac{1}{s C_{\mu }}}=g_m V_1+\frac{V_2}{R_L}$$

It's definitely tiresome to solve these manually for \$V_1\$ and \$V_2\$, but with any symbolic solver it's a breeze. (I simply wrote out the two equations in Mathematica and got the result out in one line of code.)

Answer 6

Well, we are trying to analyze the following circuit:

^{simulate this circuit – Schematic created using CircuitLab}

When we use and apply KCL, we can write the following set of equations:

$$\begin{cases} \text{I}_1=\text{I}_0+\text{I}_2\\ \\ \text{I}_0=\text{I}_3+\text{I}_4\\ \\ \text{I}_4=\text{n}\cdot\text{V}_1+\text{I}_5 \end{cases}\tag1$$

When we use and apply Ohm's law, we can write the following set of equations:

$$ \begin{cases} \text{I}_1=\frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1}\\ \\ \text{I}_2=\frac{\text{V}_1}{\text{R}_2}\\ \\ \text{I}_3=\frac{\text{V}_1}{\text{R}_3}\\ \\ \text{I}_4=\frac{\text{V}_1-\text{V}_2}{\text{R}_4}\\ \\ \text{I}_5=\frac{\text{V}_2}{\text{R}_5} \end{cases}\tag2 $$

Substitute \$(2)\$ into \$(1)\$, in order to get:

$$ \begin{cases} \frac{\text{V}_\text{i}-\text{V}_1}{\text{R}_1}=\text{I}_0+\frac{\text{V}_1}{\text{R}_2}\\ \\ \text{I}_0=\frac{\text{V}_1}{\text{R}_3}+\frac{\text{V}_1-\text{V}_2}{\text{R}_4}\\ \\ \frac{\text{V}_1-\text{V}_2}{\text{R}_4}=\text{n}\cdot\text{V}_1+\frac{\text{V}_2}{\text{R}_5} \end{cases}\space\Longleftrightarrow\space \begin{cases} \text{V}_\text{i}\cdot\frac{1}{\text{R}_1}=\text{V}_1\cdot\left(\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}+\frac{1}{\text{R}_3}+\frac{1}{\text{R}_4}\right)-\frac{\text{V}_2}{\text{R}_4}\\ \\ \text{I}_0=\frac{\text{V}_1}{\text{R}_3}+\frac{\text{V}_1-\text{V}_2}{\text{R}_4}\\ \\ \text{V}_1\cdot\left(\frac{1}{\text{R}_4}-\text{n}\right)=\text{V}_2\cdot\left(\frac{1}{\text{R}_5}+\frac{1}{\text{R}_4}\right) \end{cases}\tag3 $$

Now, we can solve :

$$\text{V}_\text{i}\cdot\frac{1}{\text{R}_1}=\text{V}_2\cdot\left(\frac{\frac{1}{\text{R}_5}+\frac{1}{\text{R}_4}}{\frac{1}{\text{R}_4}-\text{n}}\cdot\left(\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}+\frac{1}{\text{R}_3}+\frac{1}{\text{R}_4}\right)-\frac{1}{\text{R}_4}\right)\tag4$$

Using \$(4)\$, we can see that:

$$\mathscr{H}:=\frac{\text{V}_2}{\text{V}_\text{i}}=\frac{\frac{1}{\text{R}_1}}{\frac{\frac{1}{\text{R}_5}+\frac{1}{\text{R}_4}}{\frac{1}{\text{R}_4}-\text{n}}\cdot\left(\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}+\frac{1}{\text{R}_3}+\frac{1}{\text{R}_4}\right)-\frac{1}{\text{R}_4}}\tag5$$

---

Now, applying this to your circuit we need to use (from now on I use the lower case letters for the function in the 'complex' s-domain where I used Laplace transform):

• $$\text{R}_3=\frac{1}{\text{sC}_1}\tag6$$
• $$\text{R}_4=\frac{1}{\text{sC}_2}\tag7$$

So, we get:

$$\mathscr{H}\left(\text{s}\right)=\frac{\frac{1}{\text{R}_1}}{\frac{\frac{1}{\text{R}_5}+\text{sC}_2}{\text{sC}_2-\text{n}}\cdot\left(\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}+\text{sC}_1+\text{sC}_2\right)-\text{sC}_2}\tag8$$