If I replace the voltage source and 5 kΩ resistor on the left with the corresponding current source and resistor in parallel I get I = 192 µA (this is the correct answer as stated by the workbook). However, when I replace the right side current source and parallel resistor with the equivalent voltage source and resistor in series I get I = 808 µA from doing (47-2)V/(47k+5k)Ω.
Why do I get different values? Am I not allowed to transform the current source on the right in this particular circuit?
If you transform a source and a resistor then the only equivalence is the V/I characteristics at the two terminals of the transformed circuit, not for the elements inside the transformed circuit. If you transform the 47k resistor and current source to a voltage source with a series 47k resistor then the current through the 47k resistor will not be the same as it is in the original circuit.
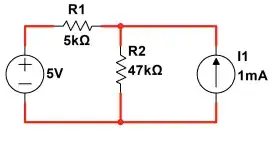
I gather you find the correct answer from this transformation:
simulate this circuit – Schematic created using CircuitLab
One way to see why is that the transformation on the left side doesn't change the circuit on the right side and the voltage difference across \$R_2\$ remains unchanged. \$I_{_{\text{R}_2}}\$ is outside of the change. So you can use usual methods to work out the current in \$R_2\$. Which you did do.
Of course, now there is a question of what happened here to \$I_{_{\text{R}_1}}\$. But since you weren't interested in that, it doesn't really matter.
In this transformation, though:
There is now your question about \$I_{_{\text{R}_2}}\$ and what happened to it. In this case, it was impacted by your transformation!
So how can we recover it?
Well, one thing you can observe here is that \$I_{_{\text{R}_1}}\$ wasn't changed, this time. It's still the same value as it was before the transition. So the current you computed here represents \$I_{_{\text{R}_1}}\$'s magnitude. It must! That fact was not lost during the transformation.
You would compute \$I_{_{\text{R}_1}}=\frac{5\:\text{V}-47\:\text{V}}{5\:\text{k}\Omega+47\:\text{k}\Omega}=-807.69231\:\mu\text{A}\$. (It's pointing opposite our indicated arrow.)
So let's return to the initial schematic you started with:
Well, now this is pretty easy. It's pretty clear that \$I_{_{\text{R}_2}}\$ must be the sum of \$I_{_{\text{R}_1}}\$ and \$I_1\$. So:
$$I_{_{\text{R}_2}}=I_1+I_{_{\text{R}_1}}=1\:\text{mA}+\left(-807.69231\:\mu\text{A}\right)=192.30769\:\mu\text{A}$$
So there it is. Recovered.
Both methods work. You just need to keep your eye on the ball. That's all.
The only guarantee you get from from replacing any section of a circuit with some equivalent, is that conditions outside that replaced section will remain unchanged. There's nothing that says the internal workings of the equivalent section must also be unchanged, or in any way related to conditions inside the original:
simulate this circuit – Schematic created using CircuitLab
Perhaps you are thinking that R3 in the second circuit is the same resistor as R2 in the first, only moved. That's wrong. Of course, it's not a coincidence that R3 has the same value as R2, but you cannot consider those two components to be the same physical device, simply relocated.
R3 has nothing to do with R2 in the original. The current through R2 in the original circuit has nothing to do with the current through R3 in the second one. The voltage across R2 has nothing to do with the voltage across R3. That's why, in my second circuit I have given this resistor a different name; it's not the same resistor.
So yes, of course you may replace the blue box with anything that behaves equivalently. You could put an elephant in there, if the result is that the rest of the world can't tell that anything changed, but your question amounts to asking why the current through R2 is not the same as the current through the elephant's trunk.
Simplifying, let the currents be in A and the resistors in \$\Omega\$, then convert back to mA and \$k\Omega\$ at the end. This unclutters the analysis.
Nodal analysis on the original circuit (sum of currents away from node = 0) gives,
$$\small\frac{V-5}{5}+\frac{V}{47}-1=0 $$
Hence, $$\small V=\frac{470}{52}=9.04\: V $$
and the current through \$R_2\$ is $$\small I=\frac{9.04}{47}=0.192\: A$$
(In real terms, \$\small I=0.192\:mA\$)
Now, converting the voltage source and \$\small R_1\$ to a current source, gives a current of \$\small 1\: A\$, in parallel with a resistance of \$\small 5\:\Omega\$.
Nodal analysis now gives (note, the 5 and 47 resistors are in parallel), $$\small\frac{V}{5}+\frac{V}{47}-2=0$$
confirming that the node voltage is still, \$\small V=9.04\: V\$, as before.
Hence, the current through R2 (converting back to mA) is, $$\small I= \frac{9.04}{47}=0.192\: mA$$
Source Transformation is not valid for the mesh in which you have a variable to calculate, if done so you will get different answers instead perform source transformation in the adjacent mesh and nodes.
