2

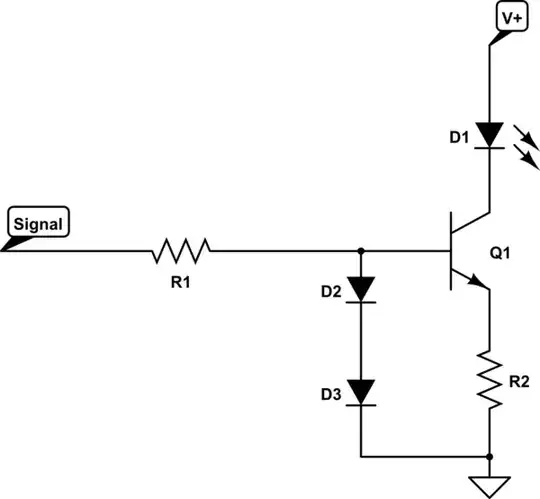
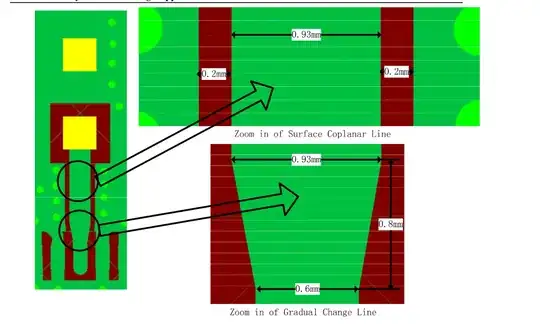
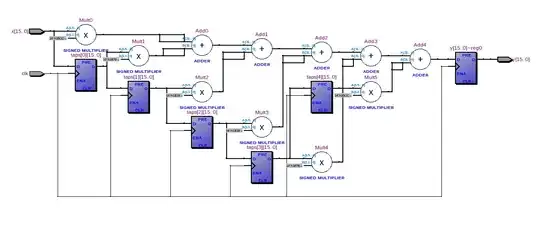
2-input XOR gate truth table enter image description here

The signal probability for a XOR gate with 2 inputs is: \$sp=(1-p_A)p_B + p_A(1-p_B)\$

3-input XOR gate truth table enter image description here

The signal probability for a XOR gate with 3 inputs is: \$sp = (1-p_A)(1-p_B)p_C + (1-p_A)p_B(1-p_C) + p_A(1-p_B)(1-p_C) + p_Ap_Bp_C\$

How to caclulate (what's the equation for) the signal probability of N inputs: \$sp=?\$

Serafeim Themis
  • 23
  • 3
  • I think your equations look faulty. Shouldn't they include the probabilities for each input signal? Try using latex to show the equation as well. Maybe you meant probability that a 2 input XOR produces a logical 1 = \$(1-p_x)p_y + (1-p_y)p_x\$ where x and y are inputs. Reference: http://www.mriedel.ece.umn.edu/wiki/images/d/db/Qian_Riedel_Zhou_Bruck_Transforming_Probabilities_with_Combinational_Logic.pdf <-- you also need to define what the truth table is for a multi-input (>2) XOR gate because it is ambiguous. \$(1-p_x)p_y + (1-p_y)p_x\$ = `\$(1-p_x)p_y + (1-p_y)p_x\$` in latex. – Andy aka Oct 26 '22 at 12:13
  • 2
    Note that the behavior of an XOR gate with more than 2 inputs is not standardized. Some interpret this as a "one and only one" function while others interpret it as an odd-parity function. It's far better if you can write everything in terms of the 2-input function. – Elliot Alderson Oct 26 '22 at 12:31
  • Related question https://electronics.stackexchange.com/questions/93713/how-is-an-xor-with-more-than-2-inputs-supposed-to-work – Elliot Alderson Oct 26 '22 at 14:01

2 Answers2

0

If you look at your 3-input XOR truth table: -

enter image description here

You can see that it can be made from two cascaded 2-input XOR gates: -

  • B and C feed XOR#1 and the output feeds an input of XOR#2.
  • The other input of XOR#2 is from A.

So, now you can derive what the probability of the XOR#2 output being 1 is. And, you can develop that further by using the same technique of cascading XOR gates and deriving the new equation.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
0

First, you can implement a 2-input XNOR gate function. XNOR gate with 2 inputs singal probability is equivalent to the sum of 2-input AND gate and 2-input NOR gate singal probabilities. After implementing the 2-input XNOR gate function, you can easily generalize your function by employing the commutative property of XNOR function. That is, calculate the signal probability for the first two inputs and after that pass that output as argument to the 2-input XNOR gate with the third input and so on. XOR signal probability can easily be calculated if you know the XNOR signal probability simply because they are complementary.

Chris vrtcl
  • 1
  • Your answer could be improved with additional supporting information. Please [edit] to add further details, such as citations or documentation, so that others can confirm that your answer is correct. You can find more information on how to write good answers [in the help center](/help/how-to-answer). – Community Nov 02 '22 at 11:28