Op-amps with negative feedback and differential amplifiers. What's the difference?

Question

I'm a physicist attempting electronics - so please bear with me. I feel I am missing something very very obvious.

^{simulate this circuit – Schematic created using CircuitLab}

An op-amp with some negative feedback (as I've drawn) will attempt to keep the inverting (\$V_{-}\$) and non-inverting (\$V_{+}\$) at the same potential. As \$V_{+}\$ increases, the output signal will increase with the differential gain. As the output increases, that is fed back to the inverting input, which will decrease the voltage differential until it is very close to zero (with some error dependent on the gain.)

Now, a differential amplifier should amplify/will amplify the difference between the two inputs, but I don't see why.

^{simulate this circuit}

Why doesn't the negative feedback force the two inputs to zero? I don't see why the same argument for the op-amp doesn't apply for the differential amplifier.

Answer 1

In the inverting amplifier the op-amp is trying to keep its -ve input at the same voltage as its +ve input. You show this as open circuit but it should be connected to ground. So the op-amp is aiming at ground.

In the differential amp the target output voltage is still a voltage that will keep the +ve and -ve inputs the same but this time the voltage of the inputs is not 0V. The voltage the inputs is at is determined by the voltage divider on the +ve input. The effect of this is to produce a amplifier where the output voltage is proportional to the difference between the two circuit inputs.

Answer 2

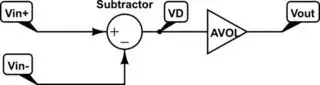
If OA2 is an ideal op-amp (no input bias currents) then the voltage at the non-inverting input is:

$$V_{+} = \bigg(\frac{V_{IN+}}{R3} + \frac{0}{R4}\bigg)\bigg(R3||R4\bigg) = V_{IN+} \cdot \frac{R4}{(R3+R4)}$$ ..a voltage divider.. and it is unaffected by the op-amp output. Where

$$R3||R4 = \frac{1}{(1/R3 + 1/R4)} $$

Similarly, the voltage at the inverting input is:

$$V_{-} = \bigg(\frac{V_{IN-}}{R2} + \frac{V_{OUT}}{R1}\bigg)(R1||R2)$$

If you don't understand the above, best stop until you do. These are just voltage divider equations you can write down by inspection.

Note that one of the two voltages (\$V_{-}\$) is a function of one of the input voltages and the output, and the other is only a function of the other input voltage.

If the op-amp has finite gain \$A_{0}\$ then

$$Vout = A_{0}((V_{+}) - (V_{-})) $$

So increasing the input voltage \$V_{IN+}\$ tends to drive the output positive, and increasing the input voltage \$V_{IN-}\$ tends to drive the output negative. Increasing the output voltage tends to drive the output negative (so we have net negative feedback, an important observation).

In the case where \$A_0\$ tends to infinity, and there is net negative feedback, and the output is unconstrained by real-world limits such as supply voltages, maximum currents etc., we can say that the difference between V+ and V- will approach zero volts. At DC that's a very good approximation for a modern precision op-amp.

So we we equate V+ and V- we get:

$$k_1 V_{IN+} = k_2 V_{IN-} + k_3 V_{OUT} $$

Or:

$$V_{OUT} = (k_1/k_3) V_{IN+} - (k_2/k_3) V_{IN-} $$

Where \$k_1/k_3\$ and \$k_2/k_3\$ are fixed constants that depend on the resistor ratios.

In the case where \$R1=R2=R3=R4\$ (or just R1=R2 and R3=R4), the output voltage is just the difference between the two input voltages.

$$V_{OUT} = V_{IN+} - V_{IN-} $$

In general though

$$V_{OUT} = \frac{R4(R1+R2)}{R2(R3+R4)}V_{IN+} - (R1/R2) V_{IN-} $$

---

As an aside, note that your first circuit does not really act as an amplifier if ideal voltage sources are applied to the inputs. The voltage at the inverting input will not change with the output voltage, so there is no feedback at all. The output will just slam from one rail to the other depending on the polarity of the difference in voltage. If you apply a current rather than a voltage (maybe from a reverse-biased photodiode detector) to the inverting input then you have a transimpedance amplifier where the output voltage is proportional to the negative of the input current.

Answer 3

Supply and demand.

The "demand" (requirement) is placed on the non-inverting input and, due to negative feedback, "supply" meets demand as seen on the inverting input equalling the the non-inverting input.

It's the same story for a difference amplifier except, the "demand" is reduced by a ratio determined by R3 and R4. So, whatever voltage is on the non-inverting input becomes the "new demand" that the op-amp tries to accommodate on the inverting input.

And, importantly for the difference amplifier, if both external inputs have the same voltage value and, both pairs of resistors (R2:R1 and R3:R4) have the same ratio, then "supply naturally meets demand" without the op-amp producing anything other than 0 volts on its output.

Answer 4

If I correct the assumed error in your 1st circuit and draw it like this instead:

^{simulate this circuit – Schematic created using CircuitLab}

Then what we have is a circuit which produces an output: $$V2 + (V2-V1)$$
Which contains the difference between the inputs as a factor, but is also offset by V2, the value at the non-inverting input.
You can weight the V1 input by adjusting the ratio between R1 & R2 which set the gain of the circuit, but with V2 connected directly to the non-inverting input you're stuck with that value as an offset at the output.

Your 2nd circuit:

^{simulate this circuit}

Produces an output which is simply: $$(V2-V1)$$
The output here is only the difference between the inputs, without an offset.
As with the 1st circuit you can weight the inputs by adjusting the resistor ratios.
If you do that you'll find that the actual output function looks more like: $$aV2 + (aV2 - bV1)$$
where
$$a = R4/(R3+R4)$$ and $$b = R1/R2$$ but for the simple case where R1=R2 and R3=R4, this reduces to the above simple difference between inputs, with no offset or gain.

Answer 5

The assumption (simplification) that we make that negative feedback forces the op amp's inputs to be at the same voltage is an approximation we make that is very useful when we try to analyse op amp based circuits to understand their operation/behavior.

In reality there will always be small difference voltage between the inputs.

In an op amp based circuit, be it an inverting amplifier, non-inverting amplifier, difference amplifier (like your second circuit) etc there are actually two gains happening simultaneously...

Firstly, there is the actual gain within the op amp. This is known as the open loop gain which is equal to Vout/(V+ - V-). This is a very high value at dc (100s of thousands) but it reduces with increasing frequency. At any particular frequency, this open loop gain has a set value whatever the particular configuration of the overall circuit. The open loop gain will vary somewhat with certain variables, such as load on an amplifier or output resistance, but essentially we can consider it to be a constant at a certain frequency whatever the circuit configuration.

Secondly, there is the gain of the overall circuit as set by the external resistor values. For your difference amplifier Vout = (Vin1 - Vin2) x (R1/R2) assuming R1=R4 and R2=R3.

The output voltage of a circuit with negative feedback (assuming that the output isn't hitting the power rail), whatever the circuit configuration, will be forced to a value which satisfies both the open loop gain value (for the particular frequency of operation) and the overall gain of the circuit set by the external resistors, known as the closed loop gain.

This situation doesn't actually occur in a perfect way. If the closed loop gain was perfectly accurate to that set by the external resistors then there would be zero difference between the op amp's inputs and the output voltage would be forced to reduce to satisfy the open loop gain. So what happens is that there is a small error in the output voltage which creates a small voltage difference between the op amp's inputs (created by negative feedback). The open loop gain is satisfied but there is a small error in the closed loop gain.

This small "error" in the closed loop gain is smaller the larger the open loop gain is at any particular frequency. Precision op amps have large open loop gains.

So as frequency is increased, the open loop gain gets smaller resulting in the output voltage also getting smaller and the difference voltage between the op amp's inputs getting larger.

The equation which relates closed loop gain to open loop gain for a non-inverting amplifier is...

Acl = Aol/(1 + B.Aol) where Acl is the closed loop gain, Aol is the open loop gain and B is the feedback fraction as set by the external resistors.

The reason the open loop gain reduces with frequency is because of the compensation capacitor (usually included within the op amp) which is there to ensure stability, but that's a whole 'nother story!

Answer 6

The infinite open loop gain part of the ideal model for an op-amp is not very useful. The discussions around the so called requirement that the input difference must be zero is a distraction. A finite gain leads to better understanding. The equation: $$V_{\text{out}}=A_{\text{VOL}}V_{\text{D}}$$

has meaning only if \$A_{\text{VOL}}\$ is finite.

^{simulate this circuit – Schematic created using CircuitLab}

The diagram shows a zero-order approximation of an op-amp. It shows two parts: a device that subtracts the inputs and a device that amplifies the difference, plain and simple. There is no mechanism or magic that requires or makes the inputs zero.

However there are some limits set by the power supplies (VCC and VEE). $$\frac{V_{\text{CC}}}{A_{\text{VOL}}}>V_{\text{D}}>\frac{V_{\text{EE}}}{A_{\text{VOL}}}$$

Whether open loop or closed loop, the equation holds for analog operation between the limits. But there is nothing restricting \$V_{\text{D}}\$'s range necessarily.