For Nyquist theorem, for channels without noise the bit rate is:
\$N=2B\log_2(L)\$
N= bit rate, B= bandwidth, L= number of levels
Intuitively I say that it should be:
\$N=B\log_2(L)\$
Indeed if L=2, every signal carries a bit, so the bit rate is equal to the baud rate. I fail to recognize from where does that 2 come from, could someone explain it?
The 2 comes from the need to avoid aliasing. Note that \$log_2(L)\$ is the sample size, and if we divide the bit rate by sample size we get the sample rate: \$\frac{2B\log_2(L)}{\log_2(L)}= 2B\$.
The formula says that bandwidth B needs a sample rate of at least 2B. You're disagreeing and saying that it just needs a B sample rate.
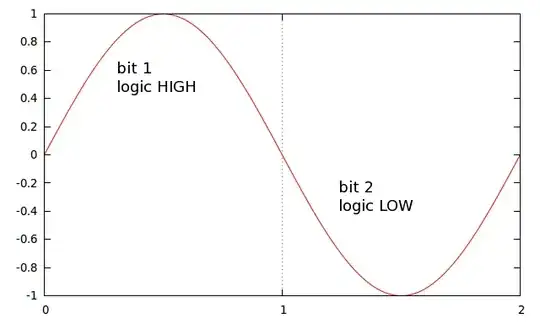
But the bandwidth is B, then it means that the highest frequency sinusoidal in the band has frequency B. If you sample such a signal with a sample rate of B, then you will not capture the peaks and valleys of the sinusoidal. The data will in fact look flat, like a DC signal! This is because you're taking a sample of the waveform only once for each period, at the same spot in its phase.
And if you sample a frequency which is just a little bit less than \$B\$, say \$B - \epsilon\$ then your sample will look like it has frequency \$\epsilon\$, and not \$B - \epsilon\$. For instance a 9700 Hz waveform sampled at 10 kHz will produce data whose most obvious interpretation is that it is a 300 Hz waveform.
This is the same effect which allows us to use a strobe light to view the vibration or rotation of a machine as if it were in slow motion. Or why, in a film, the wheels of a moving car sometimes appear to rotate slower than the forward motion, or even backwards. It is a form of aliasing.
Aliasing means that multiple original signals produce the same sampled data, so that it is ambiguous. There is always some kind of aliasing in a sampled signal, due to the use of discrete variables to represent continuous quantities. Because the amplitude is quantized, there is quantization noise: a continuous range of levels of the original signal are represented by ("alias to") the same value. Some kinds of aliasing is particularly bad, like when reconstruction synthesizes loud signal frequencies which were not in the original input, and which are in the same frequency band as the signal of interest.
You might be confusing digital bandwidth (like "2 Mbit/sec") with analog bandwidth (like "0 to 2 Mhz").
The factor two is best visible when you draw an image. The bandwidth B can at best contain a full sine wave. But a single sine wave can hold two bits: one high and one low.
I'm not a mathematician, but I guess two subsequent high bits would look similar to the red line (notice that I change the y-scale slightly for clarity):
In this image the both edges shown are identical to the original sine wave. A proper analysis program should be able to simulate that last situation in more detail. Notice that in this case the base frequency is lower than the bandwidth.
Every sample coul carry a bit only if you can sample synchronously and at the same frequency as the (single frequency) signal. But the Nyquist-Shannon Sampling Theorem (Wikipedia) applies to a band-limited signal which "contains no components higher than B Hertz".[Shannon]
Note that 2*B only applies to mathematicall "ideal" situations; real-world sampling requires sampling at rates higher than 2*B to recover all of the frequency components.
This is overly simple but should help
If the bandwidth of a channel is 10kHz and the number of levels (L) is 2 then log2(2) = 1 and....
N = 2B * 1 = 20 kbits per second.
Each cycle of a 10kHz signal comprises two parts; one that is positive and one that is negative - these two parts can by hyjacked for 2 bits of data hence 20kbits per second.
Is it possible that 2 comes in because two orthogonal waves, sine and cosine, can each carry a bit during one cycle. So for two levels and 10KHz bandwidth, the cosine carrier can carry 10kbits/sec and sine carrier can carry 10kbits/sec.
