Why does my oscillator work in LT Spice but not when I implemented it on a breadboard?

Question

I'm working on creating a phase shift oscillator that uses a common emitter BJT as the amplifier. I designed the circuit so that it produces a sine wave with a frequency of roughly 25kHz and peak to peak of 8.5 V. It works as expected when I built it in LT Spice but when I implemented it on a breadboard, I didn't get any oscillation. Is there anything that you can see in the circuit that might cause issues when physically implementing it?

Attached below is the schematic of my circuit in LT Spice as well as the output (the voltage measured at the collector terminal). Please let me know if you have any questions about the oscillator.

Do you get the DC bias voltages as calculated in the sim? (i.e. at the base and collector of Q1). Did you quadruple check your wiring? How clean is your wiring? If it's sloppy, you're creating all kinds of capacitances and inductances that you definitely don't want in an oscillator. Keep the wire runs short and neat. — Kyle B, Oct 06 '22 at 02:59
Usually high frequency circuits do not work well on a breadboard, as Kyle said, keep the wire connections short and try again. Also, the wave appears to be riding on a 4.5V DC and not 0V, not sure if that's causing some issue, maybe try playing around with your oscilloscope settings. — blackblade, Oct 06 '22 at 03:32
Apart from the 100k, the component values are not standard values. What component values did you use in your circuit'. — RussellH, Oct 06 '22 at 04:55
Snowball, Is there a reason why you want to use a high-pass version of the phase delay filter section? (It's fine. I'm just curious.) The low-pass version can be used also as a way to bias the DC operating point of the BJT, But it has it's own foibles. In any case, you need to be very delicate about the biasing pair for the BJT in a case like this. And you almost certainly need to have an emitter resistor -- though it is fine to bypass it with a cap to get lots of AC gain. (And you don't need one of the nice symmetric-looking resistors.) — jonk, Oct 06 '22 at 05:06
Snowball, If this were a nice opamp driving the triple RC network, you'd want all three sections as this is what gets you the frequency typically computed as \$f=\frac{\sqrt{6}}{2\pi\,R\,C}\$. But this is a BJT stage and there is all kinds of other loading going on that you cannot avoid. So all the nice calculations go out the window. (Or, you need to develop new ones, which is a bit of a pain here.) And so you are better off reconsidering these other details. — jonk, Oct 06 '22 at 05:11
First make sure you do have a 2N2222, and not a P2N2222 https://en.wikipedia.org/wiki/2N2222#Other_switching_transistors. — Bruce Abbott, Oct 06 '22 at 05:41
[Related Q and A](https://electronics.stackexchange.com/questions/636489/bjt-phase-shift-oscillator/636497#636497) — Andy aka, Oct 06 '22 at 09:49
You're using voltage bias on the base without feedback. That almost guarantees that the transistor in the real circuit will either be cut off or saturated. — John Doty, Oct 06 '22 at 14:17
If you vary the beta in your simulation's BJT to match the reality (either measured or from the datasheet) of your physical transistor, does the simulation still work? 0.4nF is a tiny amount and probably also does not match reality on your breadboard. — spuck, Oct 06 '22 at 15:59

jonk · Accepted Answer · 2022-10-06T09:58:46.067

This is one of those cases where less is better. Let's start out with an old stand-by BJT DC-bias circuit:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

The AC loading this presents to the passive phase-shifter is going to be painful (\$r_\pi\$ will dominate everything else about it.) But it has gobs of DC voltage gain to make up for it.

Let's start with a datasheet for an NPN: an OnSemi 2N2222A at MIT's site.

This BJT appears to just beg for a collector current of about \$1\:\text{mA}\$. And you can see that the \$\beta\$ just varies all over the place. We get \$\beta_{_\text{0}}=\sqrt{75\cdot 325}\approx 150\$ and about \$\pm\,50\%\$ variation around that figure.

Hmm, coincidentally, I just happened to use that figure, somewhere. when writing about how to bias one of these things. The number I came up with is that the collector current will vary by about \$\pm\,15\,\%\$ variation given the \$\beta\$ variation I just uncovered in the 2N2222A, above.

So, if we are going to design for \$1\:\text{mA}\$ this means we should expect up to about \$1.2\:\text{mA}\$ (rounding up) as the worst case variation in that direction and as little as about \$800\:\mu\text{A}\$ in the other direction. The design needs to accommodate that fact. It also means that the voltage gain will similarly vary by \$\pm\,15\,\%\$ around whatever we think it might be at \$I_{_\text{C}}=1\:\text{mA}\$.

The voltage gain involves a lot of minor details, like the bulk base impedance reflected to the emitter and the emitter bulk resistance. But these will be under \$1\:\Omega\$. The major detail will be the AC dynamic emitter resistance:

$$r_e^{\:'}= \frac{V_T}{I_{_{\text{E}_\text{Q}}}}$$

And the voltage gain will be:

$$A_v = \frac{R_{_\text{C}}}{r_e^{\:'}}= \frac{R_{_\text{C}}}{\left[\frac{V_T}{I_{_{\text{E}_\text{Q}}}}\right]}=\frac{R_{_\text{C}}}{V_T}\cdot I_{_{\text{E}_\text{Q}}} =\frac{R_{_\text{C}}}{V_T}\cdot\frac{V_{_\text{CC}}-V_{_{\text{C}_\text{Q}}}}{R_{_\text{C}}}\cdot\frac{\beta+1}{\beta}\approx \frac{V_{_\text{CC}}-V_{_{\text{C}_\text{Q}}}}{V_T}$$

Clearly, if we want higher voltage gain then we want to lower the collector voltage. But not too far because we have to accommodate BJT variation mentioned earlier. I'd nominally like to see the collector voltage about \$2\:\text{V}\$ above ground, suggesting a collector resistor close to \$8\:\text{k}\Omega\$. But I need to allow for that margin, so let's use \$R_{_\text{C}}=6.8\:\text{k}\Omega\$, with the idea that nominally \$V_{_\text{C}}=10\:\text{V}-6.8\:\text{k}\Omega\cdot 1\:\text{mA}=3.2\:\text{V}\$. That should be enough margin.

Given \$800\:\mu\text{A}\le I_{_\text{C}}\le 1.2\:\text{mA}\$ then we now find \$1.84\le V_{_\text{C}}\le 4.56\:\text{V}\$. That's quite a lot! (It should almost certainly be \$2.1\le V_{_\text{C}}\le 4.2\:\text{V}\$ using the 15% figure earlier.)

This then also suggests \$210 \le A_v \le 310\$. (The thermal voltage should be about \$26\:\text{mV}\$.) That's without taking any passive loading losses. That's our maximum working value.

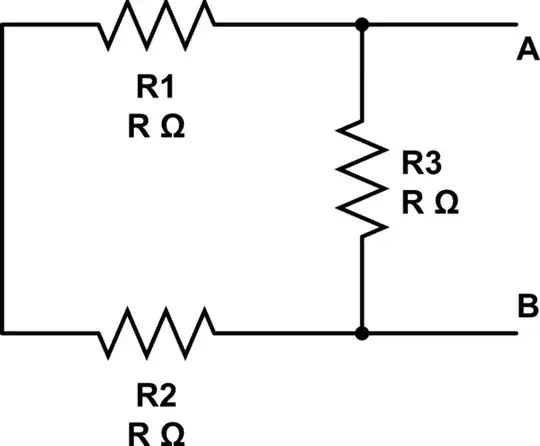
So now we are at the question of losses. But before that, let's look at your two possible 3-resistor + 3-capacitor passive networks (on the right):

schematic

^{simulate this circuit}

If we connect the top version to OUT then \$R_1\$ is just a stupid drag on the collector and reduces the signal for no good reason. Instead, if picking that one we should just kill \$R_1\$ and consider \$R_{_\text{C}}\$ as fulfilling that role.

If we connect the bottom version to OUT then \$R_3\$ is going to totally mess up the DC biasing of the BJT. The DC biasing does also represent a resistance, though. So we should just kill \$R_3\$.

Either way, you don't get to keep your pretty little passive section intact unless you bend over backwards like you did in your schematic. Which is also wrong!!

The more sensible thing to do is to remove one of the resistors at either end -- doesn't matter -- and move on. So here's the circuit:

schematic

^{simulate this circuit}

The analysis for frequency isn't so easy because \$r_\pi\$ itself will be widely varying. And I'm not going to bother with an attempt because it would at least triple what I've already written. I'll just say that you should keep the values of \$R_2\$ and \$R_3\$ above in the general vicinity of \$R_{_\text{C}}\$.

Finally, \$R_{_\text{B}}\$ should be set pretty high. Just enough to supply the needed base current at the worst case \$\beta\$. In this case, that probably means about \$220\:\text{k}\Omega\$. If this doesn't work for you on the protoboard, make it about twice that and see.

So here's a suggestion for your \$V_{_\text{CC}}=10\:\text{V}\$ case:

schematic

^{simulate this circuit}

If it doesn't oscillate either select still higher values for the base resistor or else lower the values of \$R_2\$ and \$R_3\$ to load things down a little more there.

Oh. A final note. You specified \$400\:\text{pF}\$ capacitors. If you are using a protoboard you may prefer nanofarads or higher. The boards are notorious for stray capacitance. I can't say that it matters in this case. But it is worth keeping in mind.

score 3 · Answer 2 · answered Oct 06 '22 at 03:54

C4 is unneeded, being in series with C2, and the combined capacitance is lower than 0.4nF changing the frequency and possibly increasing losses.
The 8 kΩ base-ground resistor is further lowering gain (bypassing input). Try multiplying both base-bias resistors by a factor, and see how it looks in LT Spice, then test it again.
Phase-shift oscillators need a fair amount of gain. Could the 2N222 transistor be a bit weak?

Why does my oscillator work in LT Spice but not when I implemented it on a breadboard?

2 Answers2