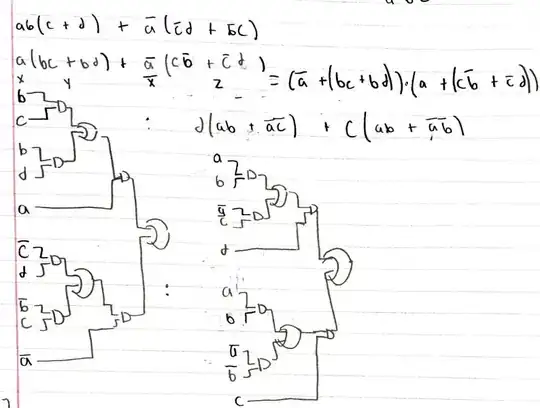
Nice question.
I'll write up an approach that I use. It's visual. I'll lead towards a solution for (B) that I like to use for cases like this. But I don't have time to work out the complete solution, since it requires an exhaustive search to complete (assuming it can be done, of course.) I don't have the time for that. But I thought I'd share something, in case it helps out.
In problem (B) you have the following minterms (a on left, d on right): 0001, 0010, 0011, 0101, 1101, 1110, 1111. Here's the hypercube with red dots on the minterm vertices:
Each NAND gate selects out all of the vertices common to two of the cubes, as you are not allowed to use a NAND as an inverter. (There are 8 cubes in the hypercube.) It acts like an OR, really, in order to do that.
For example, a NAND gate with \$\overline{c \vphantom{d}}\$ and \$\overline{d}\$ as inputs will produce a 1 for these two cubes (and all the vertices shared in common with them):

That's because \$\overline{\overline{c \vphantom{d}}\cdot \overline{d}}=c+d\$. So you get both cubes OR'd together, considering the 1 output. So 12 vertices.
(Or, oppositely, if you are considering 0 as the output, you'd get the remaining four vertices at the bottom face of the bottom cube of the hypercube.)
One NAND gate, so far.
If I now use another NAND gate (2, so far) to pick up these two:
While considering the 0 output as important so that I'm talking only about the remaining four vertices belonging to the light green highlighted face ...
This is a good moment to pause and reflect. The hypercube has eight cubes. In this situation, there are two cubes for each input: one for \$\overline{x}\$ and one for \$x\$, whatever \$x\$ represents as an input. Since there are four inputs, there are eight cubes. And for any given input, the two cubes it represents are on cubes that are diametrically opposite each other on the hypercube.
The above indicated NAND gate is really one of two possible interpretations:
On the right, we are saying that we get a 0 when intersecting the \$\overline{c \vphantom{d}}\$ and \$\overline{d}\$ cubes. Those cubes are the cubes directly opposite the ones I just showed in the above illustration, and the intersection of those two are the four vertices highlighted by the light green face. (The answer I'm looking for.)
On the left, we are saying that we get a 1 when taking the union of the \$c\$ and \$d\$ cubes. In this case, that's not what I care about.
So the point here is that you get to decide which interpretation you are looking for by selecting which of the two visions matter to you. But you also have to take the output condition, too. You do get to choose your interpretation, but you don't get to choose the output you get for that choice. There are two possible outputs (binary, after all) and therefore two interpretations. How you use the output, later, will matter.
... and then use a NAND gate (3, so far) to pick up these two:
While considering the 0 output as important so that I'm talking only about the remaining four vertices belonging to this other light green highlighted face ...
... then I can use another NAND (4, so far) to sum these two pairs of four vertices.
I only want six of the eight, though. So now I use another NAND (5, so far) to intersect these 8 vertices with the earlier 12 vertices I kept from the first pair of cubes, leaving just six.
Now there's just one more vertex to get. The arrow on the following image shows you which one is still missing from the logic:
I've used (5) NAND gates, leaving just (3) NAND gates to meet the requirement. But I'll have to visualize a method to pick up that last point. Or perhaps find a different visualization than I used above to get here.
Here's the diagram up to this point:
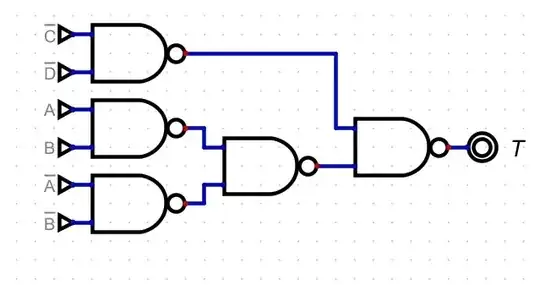
\$T\$ will be 0 for those six vertices I captured. This is a perfect feed in, into another NAND gate (6, now), to get the desired 1 -- if you can figure out how to capture that last point and provide a 0 into the other input to the NAND with the remaining two NANDs available to you.
Here's an annotated version:
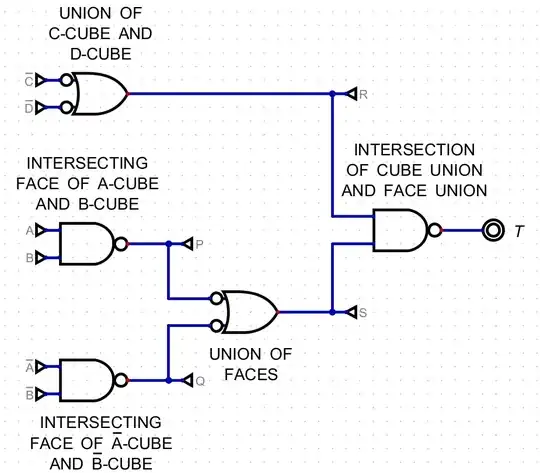
At this point we have access to the following information:
- \$\overline{P}\$: Four vertices at the intersection of the \$a\$-cube and \$b\$-cube.
- \$P\$: Twelve vertices from the union of the \$\overline{a\vphantom{b}}\$-cube and \$\overline{b}\$-cube.
- \$\overline{Q}\$: Four vertices at the intersection of the \$\overline{a\vphantom{b}}\$-cube and \$\overline{b}\$-cube.
- \$Q\$: Twelve vertices from the union of the \$a\$-cube and \$b\$-cube.
- \$\overline{R}\$: Four vertices at the intersection of the \$\overline{c\vphantom{d}}\$-cube and \$\overline{d}\$-cube.
- \$R\$: Twelve vertices from the union of the \$c\$-cube and \$d\$-cube.
- \$\overline{S}\$: Eight vertices composed from the union of four vertices from the intersection of the \$\overline{a\vphantom{b}}\$-cube and \$b\$-cube and four more vertices from the intersection of the \$a\$-cube and \$\overline{b}\$-cube.
- \$S\$: Eight vertices composed from the union of four vertices from the intersection of the \$a\$-cube and \$b\$-cube and four more vertices from the intersection of the \$\overline{a\vphantom{b}}\$-cube and \$\overline{b}\$-cube.
And of course \$T\$ and \$\overline{T}\$ (opposite meaning.)
This is where I leave it to you. I don't want to take more time on this and I'm assuming that the problem can be solved. But I did want to show how to visualize the use of NAND gates as you try to capture the terms you want.
Just as a final note, here's a diagram showing the edges emanating from the remaining point (four edges) and the six surfaces (faces) that are thereby defined by pairs of edges:
That may help in considering some approach to reach that point.
Personally, this is how I think. I don't think in terms of algebra, which I believe hides and muddles things behind a wall of text that can be almost indecipherable. If you follow all the rules, you get the right results. But it often leaves one without any real vision. It's just rote work. Seeing things in terms of geometry, rotation, dynamic shape transformations, etc., provides a path for deep insight into problems. That doesn't mean algebraic manipulation isn't important -- it is very important. It just means that being able to see is just as important, if not more-so, as often the algebraic approach to a problem can be seen visually first, leading to insights that guide how to better state the algebraic problem.