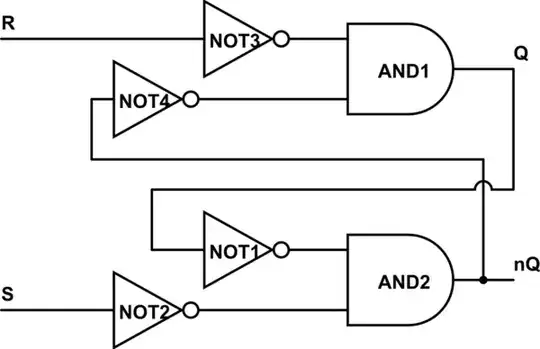
When placing a frequency-dependent resistor in LTspice using the Laplace statement the result of an ac simulation (right circuit) looks fine:
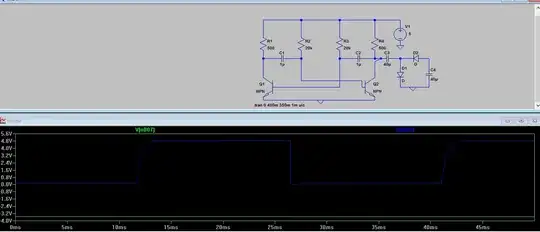
However, when I use the same frequency-dependent resistor in a noise simulation (left circuit) the result is wrong (e.g. I would expect approx. 1 nV/sqrt(Hz) at 50 Hz):
Am I doing anything wrong or does LTspice just not support frequency-dependent resistors in a noise simulation?
Edit (s/sqrt(-1) instead of abs(s)):