6

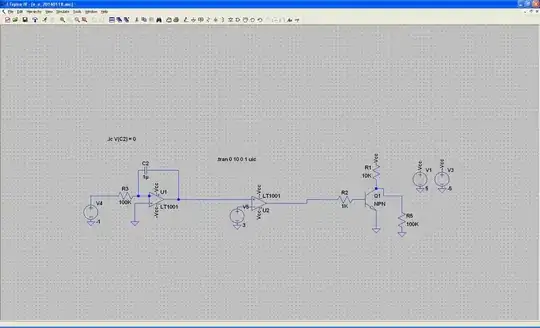
I have designed a buck circuit.

The Bode plot of my system is as follows:

enter image description here

I use a type Ⅲ compensator to control my system. The switching frequency is 100 kHz. The cut-off frequency is 20 kHz and the phase margin is 60°.

The transient state of the system does not meet my requirement: when the load is from 100% to 50%, the output can't exceed 12.12 V, but as the plot shows, the max of the output is almost 12.37 V.

I have tried increasing the phase margin (from 60° to 80°) and lower the cut-off frequency (from 20 kHz to 10 kHz) (these methods could improve the damping of the system and reduce overshoot, right?), but the effect is limited. So what else could I do? Could anyone give me some suggestions?

enter image description here

Second Edited：

Thanks to Verbal Kint's book, I have done something to improve the transient response including using two parallel capacitors rather a big capacitor to lower the ESR of the capacitors and increasing the cut-off frequency \$fc\$ (\$fc\$ must be higher than the resonant frequency \$fo\$ of output impedance).Now the \$fc\$ is 30kHz.

Now The main circuit is as follows: enter image description here

And now my circuit's transient response is as follows: enter image description here

when the load is from 50% to 100%, the response is in my expectation: the decrease of Vo is less than 120mV, but when the load is from 100% to 50%, the response still doesn't meet my requirement. I think I can't increase the cut-off frequency \$fc\$ any more, because the nyquist show me that it will become unstable when I increase \$fc\$!! Now what should I do? Thanks for help!

T L
  • 475
  • 1
  • 8
  • 4
    What circuit? Looks like voltage mode control. Looks like filter transient is blowing out your spec, try lower Zo instead (lower L, higher C). If L is limited by current ripple or staying in CCM, then Fc will have to drop. This, and the complexity of the compensator, are strong reasons to prefer current mode control. – Tim Williams Sep 24 '22 at 04:47
  • Thanks! The Buck converter works in the CCM and in voltage mode control. I have tried to drop the cutoff frequency to decrease the overshoot but the effect is limited. I haven't tried current mode control before. So your suggestion is using current mode control rather than voltage mode control? Could you please explain a little bit about using current control rather than vlotage mode control? – T L Sep 24 '22 at 06:48
  • 4
    A schematic diagram would be welcome to see how you've arranged things. What matters is not the open-loop \$Q\$ of the \$LC\$ filter but the small-signal *closed-loop* output impedance of your circuit. It is the one dictating the transient response, as long as the circuit remains linear of course. Did you plot the output impedance with your control strategy? Also, what parasitics did you model in the output capacitor? You can have a look at my [APEC 2012 seminar](https://cbasso.pagesperso-orange.fr/Downloads/PPTs/Chris%20Basso%20APEC%20seminar%202012.pdf) where I tackled the subject. – Verbal Kint Sep 24 '22 at 07:11
  • @Verbal Kint. Thanks! Still studying your book to try to solve my problem. I meet some problems. In the Chapter 3 in your book , is the formula (3.189) incomplete? It seems that you leave out the term "Vout(s)"? – T L Sep 26 '22 at 06:46
  • Glad to know you are looking into this. Yes, the \$V_{out}(s)\$ term is missing in (3.189), thank you for pointing this out. You could perhaps update the post by including the schematic diagram of your buck converter and then we could advise some improvements to the compensation strategy? Thank you. – Verbal Kint Sep 26 '22 at 20:08
  • @Verbal Kint. Thanks! Your book helps me a lot. The response when load is from 100%-50% meets my requirement, but when load is from 50%-100%, the response doesn't meet the requirement. I have renewed my question, could you help me see again？ – T L Oct 03 '22 at 09:20
  • 1
    Regarding stability: you're adjusting the compensation values while doing this, right? – Tim Williams Oct 03 '22 at 09:34
  • I designed the compensation according to the worst case (I compared the phase margin under different input and load conditions to determine which is the worst case). Then I didn't change its parameters. – T L Oct 04 '22 at 08:23
  • 1
    @TL, you would first need to disclose how you did built the compensator and what model you did use for the op-amp. The absence of symmetry could come from a different response of this section or a saturation. Please check my [free templates](https://cbasso.pagesperso-orange.fr/Downloads/Book/Christophe%20Basso%20SIMPLIS%20Collection.pdf) as I have a closed-loop buck also. The reaction mechanism is different when the load is released and explains the lack of symmetry, especially in large-signal situation. Try also to narrow the output current dynamics to limit the error excursion. – Verbal Kint Oct 06 '22 at 16:20
  • @VerbalKint Thanks sir! Now I have solved my problem by studying your book! I wrote an answer about what I learned from your book (although I don't know whether I understand it right.) and I am still reading your book to learn more! – T L Oct 07 '22 at 00:56

2 Answers2

2

The initial voltage spike at load step from 100% to 50% mainly depends on the inductor and the output capacitors. The inductor will dump excess energy into the output capacitors and increase the voltage at the output. Like already suggested in the comments, either decrease L or increase C to decrease the voltage spike.

The controller behavior is only kicking in some microseconds after the initial voltage spike.

Lars Hankeln
  • 2,513
  • 1
  • 8
  • 15
2

Thanks to Mr. Christophe's Book Designing Control Loops for Linear and Switching Power Supplies A Tutorial Guide! Now I have solved my problem. Now I plan to write a brief answer to show how I solve my problem. Hope the answer will help you too.

I got a task that the total ripple must be within 120mV when the load is from 100% to 50% and from 50% to 10%.

When I designed the circuit according to the requirement of output ripple and the inductor current, I tested the circuit's transient response. then I got a figure like this:enter image description here

The voltage spike was too huge for me. What did I do first? I increased the phase margin and decreased the cut-off frequency \$fc\$. The increased phase margin did help me but the effect was limited. But when I decreased the \$fc\$, the spike was even higher which confused me because I thought the lower the \$fc\$ was, the higher the damping was.

After studying the book, I checked out the spike when the load was from 50% to 100%. The output voltage consist of two part (don't consider the ESL of capacitor): the voltage drop across the ESR of capacitor and the vlotage drop due to capacitor.

The voltage drop across the ESR is a slope. The value is about the \$ΔVESR = ESR*ΔIout\$. The ESR of my output capacitor was two big that no matter how I compensated the circuit, the spike always was too high. To lower the ESR, I used several parallel capacitors to replace one capacitor utill the ESR was small enough.

The second part of volatge drop was purely because of the capacitor. The value is about \$ΔIout*Zout(fc)\$. As for Buck circuit, there is a equation: \$ Zout(fc) ≈ sqrt(1/(2π*fc*Cout)^2+r^2)\$ . According to the requirement of voltage sipke, you can get the maxinum Zout. First I change the cut-off frequency \$fc\$. The cut-off frequency \$fc\$ has an influence on the \$Zout\$. According to the the maxinum Zout, solve the equation: \$ Zout(fc) ≈ sqrt(1/(2π*fc*Cout)^2+r^2)\$. I get a mininum value of \$fc\$. Then use the compensator to set out a \$fc\$ that higher than the mininum value.

When I run the simulation. I get a figure like this: enter image description here

The volatge drop meets my requirement when the load is from 50% to 100%. But when the load is from 100% to 50%. Why are the two processes different? Aren't they supposed to be symmetrical? This is my guess: when the load is from 50% to 100%，the energy (I use \$W1\$ to represent it) that the load need is suppied by capacitor and inductor. The energy \$W2\$ that the capacitor supplies is less than \$W1\$. When the load is from 100% to 50%, the excess energy W1 of inductor will all come to the capacitor. It is clear that the value of voltage drop caused by \$W2\$ is smaller the the value of voltage rise caused by \$W1\$. And according to this guess,to drop the voltage spike, I could decrease the value of inductor or increase the value of capacitor.

Because I don't want to decrease the value of inductor to avoid increasing the inductor current ripple, I increase the value of output capacitor. And finally the circuit meets my requirement!

T L
  • 475
  • 1
  • 8