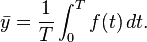I learned that the Ebers-Moll equation Ic = Is(T) ∗ exp(Vbe/Vt) "predicts" the collector current to rise exponentially with the base-emitter Voltage.
Experimenting with LTSpice for a LED current sink I apparently ran into the limits of the Ebers-Moll model / equation:
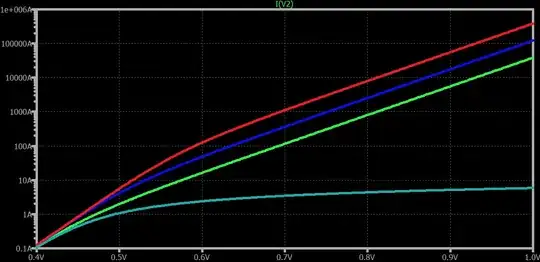
Instead of a straight line into ... lets say to 1000 A, there is a knee at around only 100 mA to 1 A.
I didn't expect to hit the limits of Ebers-Moll at such "low currents". Assuming the simulation results are correct.
This doesn't look like the early effect either. I don't know what's happening here.
Switching to a "more powerful" transistor doesn't show different results, nor does increasing R1 to 0.1 Ohms.
Did I run into the limits of the Ebers-Moll equation at around 100 mA? Or did I make a mistake?
Could somebody please explain what limit I ran into here? Why is the current not increasing exponentially anymore?
What model explains this effect?
Thanks!