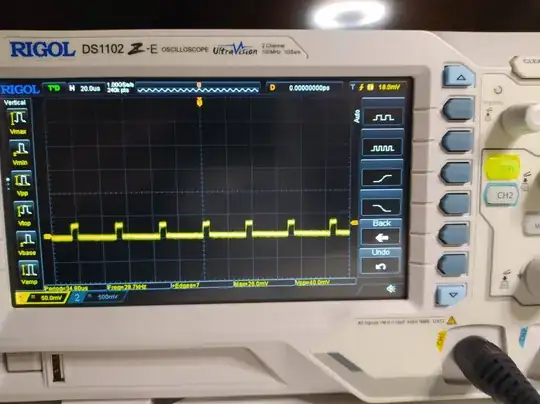
Crystal oscillator with inverter gate, crystal engraved with "1 MHz" outputs 1.68 MHz

Question

I have been playing with my favorite clock oscillator circuit:

^{simulate this circuit – Schematic created using CircuitLab}

using various crystals. One of them has "1.00 MHz" engraved on it, this one:

but it clocks at 1.84 MHz.

it's not the scope settings, as the 2, 4, 8, etc. crystals are all performing as declared.

1. Is my crystal just bad?
2. Do I misunderstand something? -- I darkly remember that the frequency rating of crystals has 2 different variants of some kind.
3. Am I doing something wrong? -- particularly, I often see additional capacitors used like so:

^{simulate this circuit}

Are those capacitors mandatory? And how are they dimensioned?

I use R1 = R2 = 1 kΩ I don't think that they are causing something to go wrong for 1 MHz when it works for everything else?

I have also tried 74HC04, 74LS14, 74HC14, and nothing works as reliable (until 16 MHz) than the 74LS04.

Answer 1

I am, frankly, not sure why your circuit works for you at all, with any crystal. Presumably it's intended to work at or near the crystal's series resonance. In my experience, if you get a crystal oscillator circuit wrong it'll often oscillate at some random frequency determined by everything else in the circuit but the crystal.

The classic circuit to use with a crystal specified for parallel resonance uses one inverter, not two. Possibly followed by a (not shown) buffer to clean up the signal before driving anything else.

The reasoning behind this is that at a crystal's parallel resonance point it acts like an inductor, so the two caps and the crystal look like a pi filter, with 180 degrees of phase shift -- in order for the circuit to work, the amplifier needs to supply another 180 degrees of shift which it does -- if it's inverting.

The 74LS04 or 74C04 should work fine. They work because they aren't actually "perfect" logic chips -- they have an operating range where they behave like linear amplifiers.

The 74HC04 is more perfect as a logic chip -- it is actually three inverters in series inside the chip. This is so that it gives a nice crisp output. It also, unfortunately, makes it no longer work as a straight amplifier. To answer this problem, the manufacturers make a 74HCU04, which acts more like a 74C04 and works great as a crystal oscillator amplifier.

The circuit shown is the "one size fits all" version.

Pick C1 and C2 to be roughly twice the crystal's load capacitance, minus the expected parasitic capacitance of board and inverter (just assume 5pF if you don't have a number). If you need high precision, you can bend the frequency up or down by choosing different C1 and C2 values.

For CMOS, R1 should between 100k\$\Omega\$ and 1M\$\Omega\$. For 74LS, it should probably be around 10k\$\Omega\$ or so (I can't remember the best number).

As mentioned in the comments, for a series that has a strong drive, like 74HCU, you need R2 -- it's value depends on the crystal you use, but 2k\$\Omega\$ to 5k\$\Omega\$ is probably in the ballpark (for production, find the largest value that'll ensure reliable operation over temperature, then go with two to four times less that -- for extra reliability dig into the literature and figure out how to insure that the crystal drive isn't too high).

^{simulate this circuit – Schematic created using CircuitLab}

Answer 2

Having read through the answers and links provided by @Justme I sense there is confusion about what it means when a manufacturer specifies that a crystal operates in "parallel resonance". I don't like the term because it creates confusion over whether it means: -

1. The natural parallel resonance of the crystal (also called antiresonance) or
2. Adding "parallel capacitance" to the crystal to make it resonate

To enhance the confusion, "adding parallel capacitance" inevitably means that the oscillator's running frequency is normally closer to the natural series resonant point.

The manufacturer's term "parallel resonance" is also confusing in another way because, putting capacitors on both sides of the crystal turns the circuit into a π-filter and clearly, both capacitors are grounded i.e. not parallel with the crystal.

Conclusion: manufacturer's ought to be clearer about what they mean.

---

This micro-cap simulation looks at the impedance of a raw crystal to try and get to the bottom of what might be happening: -

The equivalent circuit values were chosen based on a survey of various manufacturer's data. There are two interesting points in the spectrum. Both are pretty close; one at 10.000 MHz (the natural series resonant point) and, one at 10.004 MHz (the natural parallel or antiresonance point).

With input and output capacitors and series resistor R1 we can plot the transfer function: -

Its optimum operating frequency is offset from the natural series resonant point by a small amount (i.e. this crystal might be labelled as being 10.00118 MHz): -

As can be seen, the steeper the phase response (as it passes through 180°) the less ambiguous is the operating frequency i.e. the preferred area to operate is closer to natural series resonance (10.000000 MHz) on the left.

So, the crystal and the two external capacitors form a π-filter. Manufacturer's calling them "parallel capacitors" is lazy and misses the point because, both capacitors are grounded <-- it's a π-filter!!

Hence, because most crystals are designed to operate closer to their natural series resonance, the preferred phase shift is 180°. This then means that adding an inverter such as the SN74LVC1404 will make the circuit reliably oscillate: -

Of course you can use an unbuffered "04" device or even a buffered "04" device but, you won't get the best frequency accuracy and drift. Does that matter; not much if the timing isn't critical.

Is my crystal just bad? Do I misunderstand something? Am I doing something wrong?

1. Probably not
2. Probably
3. It's not wrong if it works for you (but I wouldn't do it this way)

Images came from my basic website.

Answer 3

Note that C2 doesn't do much of anything, if that side is hard driven by the logic output. A series resistor between this node, and the gate output, is usually seen; typical values are on par with the impedance of the crystal itself, so, a kohm or thereabouts. This also sets drive level (power), which is important for smaller crystals. Then the C-crystal-C motif can be used, and works as usual.

(Specifically what's happening, with this capacitor-loading pi network, is the crystal's impedance is inverted: thus a series-resonant crystal acts like a parallel-resonant tank, giving maximum feedback at the tuned frequency.)

Likewise R2 I think doesn't do anything, as it's strung between two outputs. R1 is usually much larger (a meg for CMOS, maybe 10-47k for LS?).

Without the usual impedance environment around the crystal, it could be that other modes are stronger than the intended fundamental, and therefore starts up at another frequency. A crystal is not just one resonance, but a tiny forest of peaks; normally, most of those peaks are below the fundamental so they die out as the fundamental is repeatedly amplified. But the relative amplitudes depend on the surrounding impedance.

Something else you can do to ensure startup in a band -- particularly important for overtone crystals, where the fundamental is still strong but operation at an overtone is desired -- is place a resonant tank in the feedback loop. Usually a parallel tank in parallel with the crystal, but a series tank shunting one or both sides can also be used. Ballpark, choose L and C such that \$Z_0 = \sqrt{\frac{L}{C}}\$ is around the crystal impedance (so, a kohm -- give or take the desired Q factor, lower for parallel, higher for series), and \$F = \frac{1}{2 \pi \sqrt{L C}}\$ equal to the desired tone.

Just for playing around, it should do well enough to pick a few reasonable inductor values (say 22 to 220 µH) and adjust capacitance until you get the right peaks -- play around and see how it varies with capacitance, in operation (it should hang onto a given tone over a relatively wide range, once running) or from cold startup (which should be more sensitive as far as selecting a given tone).

Answer 4

^{simulate this circuit – Schematic created using CircuitLab}

Try separating the biasing of the two inverters with a capacitor (C1).

The 1MHz crystal might be a series resonant type, in which case C2 can be replaced with a short circuit.
More commonly, the crystal is a parallel-resonant type and requires a small-value series capacitor (C2) to adjust frequency exactly. Don't forget to connect a 100nf bypass capacitor between pins 7, 14!

---

Shown below is a PCB version using a 1.8432 Mhz crystal. Series capacitor C2 was about 50 pf. Scope image is from input pin of first gate (yellow), first gate output (cyan). Threshold voltage of the 74LS04 (actually, I used a 74LS00) is about +1.3V.

Start cursor [S] is at +1.32V near the threshold voltage of 74LSxx logic, while end cursor [E] is at +5.0V which is Vcc applied to pin 14.

---

Note that just a little capacitance is needed in the feedback path to oscillate. For 74LSxx logic, a bit of capacitive-coupling (output-to-input) caused oscillation in the 20-30MHz region.
Since a crystal includes a parallel capacitance, as well as a series RLC resonator, this kind of oscillator is vulnerable to oscillate off-resonance. If crystal activity is poor, its parallel capacitance might dominate over series resonance. For example, a 100kHz crystal was substituted. Its parallel capacitance was measured at 7.4pf. Oscillation frequency was an unstable 23 MHz. rather than the desired 0.1 MHz.
Breadboard construction is risky where stray capacitance can influence operation.

Answer 5

1. Crystal may or may not be bad. If you don't know the crystal type then it might not work properly in the circuit you built.

2. Correct; there are crystals that are manufactured to operate at the frequency printed on it in series resonance, and others need to be operated in the "area of usual parallel resonance", when it has the correct load capacitance.

3. This seems like a mixture of incompatible oscillator circuits.

The basic thing is, your circuit is intended for series resonance because crystal is over two inverters, and since the inverters are biased with 1k it means the circuit should use LS04 type inverters.

It might be a good circuit, but in practice, a Pierce oscillator should be relatively simple to get working. Best to use unbuffered CMOS inverters like HCU04 but it can work with HC04 as well if it has a series resistor.

Also, the circuit is built on a breadboard, which is a very poor platform for sensitive circuits like this, due to stray capacitances and inductances.

Answer 6

• I'm surprised you got anything to oscillate

• or burnt out the Xtal >50 uW.

  • ( the high Q puts > 10kV on internal motional lattice driven from low impedance and series load, which explain some idea how >50uW can be a threat to damage.

Try any 1 CMOS inverter only.

I can' t recall if KDS ever made series mode Xtals.

Answer 7

Crystal oscillators are difficult to calculate component values for. They are very misunderstood by many.

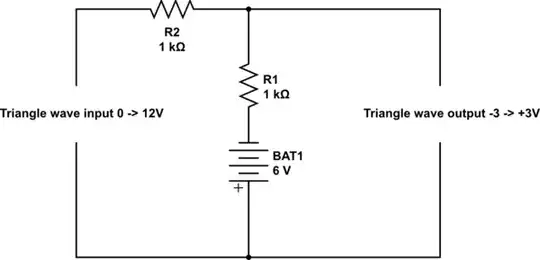
The phase shift from input to output of a non-inverting amplifies is 0 degrees. Therefore the phase shift through the feedback network must also be 0 degrees.

If a series RLC network will provide zero degrees phase shift at resonance so connecting it between output and input of a non-inverting amplifier will allow oscillation at the resonant frequency defined by L and C. But only if the loop gain (from input to output and back to the input) is greater than or equal to unity.

^{simulate this circuit – Schematic created using CircuitLab}

In the OP's first circuit, the input impedance of the two inverters is a capacitor in parallel with a resistor. Each of these will introduce a phase lag resulting in either a frequency shift or ceasing oscillation altogether. Also there is a propagation delay across each inverter that also causes a phase lag. The feedback resistors are to bias the amplifiers into their linear region. They also reduce the input resistance of their respective inverters. The capacitor between the inverters is for bias isolation.

To compensate the frequency will shift toward the inductive side of the RLC network and so be slightly off resonance for the RLC network, but not the oscillator. A capacitor can be used in series with the RLC network to provide a phase lead bring the RLC network back onto resonance.

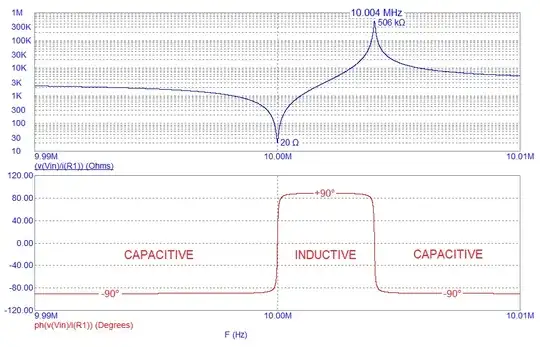
So the crystal is operating as a series RLC network for the noninverting configuration. Parallel resonance will not work for this configuration.

The OP could place a capacitor in series with the crystal to adjust the frequency. The crystal operates as an inductor in series with C2. Sorry I do not have a calculation. Perhaps a value between 10pF and 50pF would work. I do not have a lot of experience with this configuration so I don't know how robust it is.

The OP's second circuit is not used for crystal oscillators.

^{simulate this circuit}

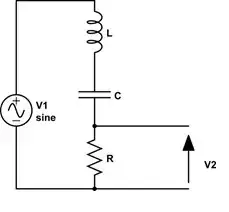
This diagram demonstrates the standard single inverter crystal oscillator. Rin and Cin are internal to the inverter and are shown external for discussion. R1 provides feedback to bias the inverter to the middle of its linear region.

Ideally the inverter provides a 180 degree phase shift. So the feedback network must also provide 180 degree phase shift for a total of 360 degrees. So the crystal must operate at parallel resonance. The crystal is essentially a second order RLC network so it can provide a 180 degree phase shift at parallel resonance. Or can it?

There's more, as before the inverter has a propagation delay and Rin//Cin adds more phase lag, so actually phase lead is needed to get it right. The crystal must operate in the inductive region between the resonant points in the presence of the series combination of C1 andC2 in parallel with the crystal's lead capacitance. Th crystal operates as an inductance in parallel with C! in series with C2.

But that still may not be enough. If the phase lag is too great then we need a way to get more. This is the purpose for Rs. Rs includes the output resistance of the inverter, so may not be needed. This turns the feedback network into a 3rd order system which in theory can provide up to 270 degrees of phase shift.

I was always told that Rs was to control drive power. It may do that but I think the added phase control is more important.

So in any case the crystal does not operate at its series or parallel resonance. It acts as an inductive element.

I do not have calculations. I do simulation and experimentation. Where microcontroller oscillators are concerned I do as the datasheet tells me. Several years ago I did a simulation in Octave. I looked it up for this poste but it wasn't working. When I get it working again I will update this post.

Cheers

Answer 8

^{simulate this circuit – Schematic created using CircuitLab}

You've missed only a capacitor. ^^ It is from a Commander 2 (1541 clone) disk drive and it is working :-)