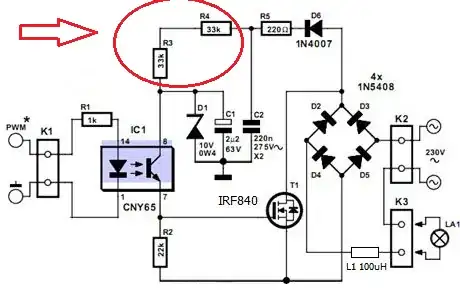
Trying to understand what is the maximum and minimum for the input signal of a differential pair by solving this example below.
My solution: To let the circuit operate as a differential pair, it must be in an active region where $$ VCE> VCE(sat)$$
by considering $$ VCE(sat)=0.5V$$ and $$ IC_1=IC_2=1mA$$, and solving in DC bias
$$VC_1=20-(15k*(1mA))=5V$$ $$VB_1=\frac{20*5k}{15k+5k}=5V$$
So, $$VE_1=VB_1- VBE_1=5V-0.7V=4.3V$$. As $$VCE_1 (0.7V)> VCE(sat) 0.5V$$ and it satisfies the condition, I will consider what would jeopardize this equation! It will not be in the active region if $$ Vo=VE_1+VCE_1(sat)=4.3V+0.5V <4.8V $$
By considering $$ Vo=Ad_1 *Vd+Acm_1*V_cm$$ Then, $$Vo=\frac{R_{c1}}{2r_e} * vi +\frac{R_{c1}}{r_{e1}} * \frac{vi+0}{2} $$
By placing the values $$4.8V=\frac{15Kohm}{2*25 ohm} * vi +\frac{15k Ohm}{25 Ohm} * \frac{vi+0}{2} $$ I expect to get the maximum of vi=8mV.
I know that there must be a minimum value that stops the differential pair Q1 from acting as a switch and being turned off, but not sure how to approach that.
"Solution" The correct solution to Vi(max) is as follows but I cannot understand and am not sure why my solution is wrong: