0

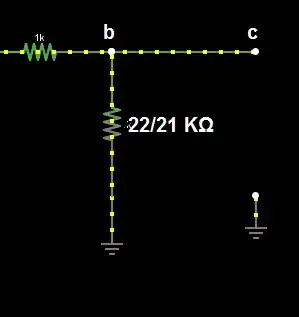
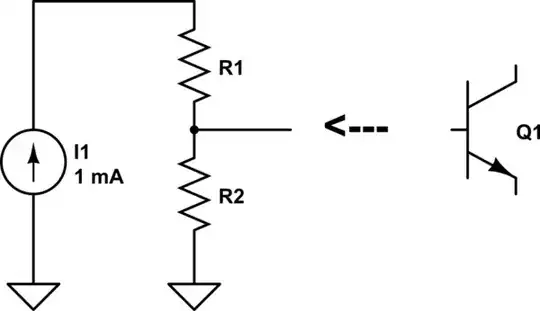
I know (from the textbook) the Thévenin expressions for the circuit from reference terminals b-b' are

$$V_{th} = V_{CC}\frac{R_2}{R_2+R_1}, R_{th} = R_1//R_2$$

But I'm not understanding how one gets there. How are the resistors parallel from the point of view of b-b'? The fact that \$R_1\$ is in a node that extends "behind" the reference terminals b-b' is really confusing.

And how come \$V_{th}\$ is a voltage divider if there's a current \$i_B\$ splitting into the B of the transistor and \$i_2\$ to GND? Also, how would a resistor at \$i_C\$ change the expression?

Is there another format to "see" this more obviously? I tried but couldn't simplify in a way that made sense to me from previous Thévenin problems.

enter image description here

ludicrous
  • 965
  • 1
  • 10
  • Here you will find the answer https://electronics.stackexchange.com/questions/471906/calculation-of-base-current-and-what-decides-the-current-through-collector-emitt/471923#471923 Andy additional questions? – G36 Aug 31 '22 at 15:17
  • In addition, look [here](https://electronics.stackexchange.com/a/337018/38098). :) And ludicrous? R1 and R2 are in parallel because your Vcc supply is 0 Ohms. A Vcc supply is both a direct short and also a voltage difference. – jonk Aug 31 '22 at 19:28

2 Answers2

2

The resistors are effectively in parallel because the voltage source Vcc is "stiff". If you try to change the voltage at b relative to b' then current through both resistors will change- the conductances add, the resistances are in parallel.

If the bias network looked like this:

schematic

simulate this circuit – Schematic created using CircuitLab

Then the Thevenin resistance would be R2 and the Thevenin voltage I1*R2.

With regard to your second question, when considering the Thevenin voltage, the current Ib is not there. You're only looking at three parts- the voltage source and the two resistors. Thevenin voltage is the open-circuit voltage.

Once you simplify the circuit to a single resistance R1||R2 and the Thevenin voltage source you can mentally reconnect it to the base.

Spehro Pefhany
  • 376,485
  • 21
  • 320
  • 842
  • I see! How about if I had a resistor at Ic, how would I handle it? Because now it is "linked" to the back of b-b' – ludicrous Aug 31 '22 at 15:42
  • Nothing connected parallel to the voltage source will change the voltage. If you add a resistor in series that is affected by Ic then it's a different kind of problem. – Spehro Pefhany Aug 31 '22 at 16:30
1

What you do is take the circuit Vcc, R1 and R2 as a separate from the rest of the circuit and find it's Thévenin equivalent, then you connect that with the rest of the circuit and figure out the rest. The base current \$i_B\$ is accounted for after you have the Thévenin equivalent of the bias divider.

When finding the Thévenin equivalent resistance you short voltage sources, so with Vcc shorted R1 and R2 are in parallel.

GodJihyo
  • 17,628
  • 1
  • 16
  • 45