DC offset of DC signal with op-amp

Question

I have a DC signal from a DAC in the range of [0:3,3]V and want to convert it to be in the range [-5:5]V. My approach would be to scale with op-amp with gain 3 and then DC offset.

I've read that this could be done simultaneously by using an op-amp. By using inverting amplifier with gain 3 but instead of grounding the noninverting terminal apply biasing voltage connected to a voltage divider.

After that I can use an inverting buffer to make the map correct (0 to -5;3.3 to 5.)

Is this how this would be done? Should I apply negative bias voltage to bring the midpoint of my range down? Are there any additional things to consider?

Answer 1

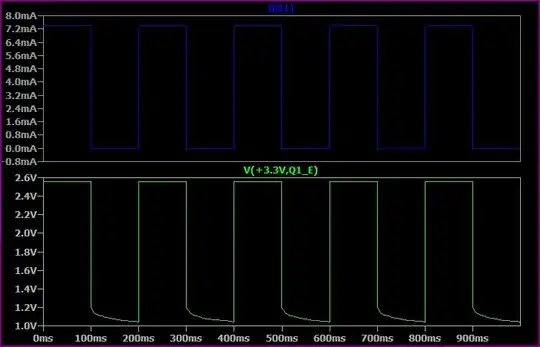
The relationship between input \$V_{IN}\$ and output \$V_{OUT}\$ is:

$$ \begin{aligned} V_{OUT} = 3(V_{IN}-1.65) \end{aligned} $$

Here's a single op-amp solution:

^{simulate this circuit – Schematic created using CircuitLab}

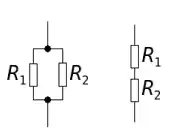
This is a non-inverting amplifier with gain \$1+\frac{R_2}{R_1} = 3\$. That's the factor of 3 we needed. The offset is provided by the voltage source 2.475V, which is not so obvious. The complete relationship between input and output for such a design is:

$$ V_{OUT} = V_{IN}\left(1+\frac{R_2}{R_1}\right) - V_{OFS}\frac{R_2}{R_1} $$

I simply plugged in a known input value for \$V_{IN}\$ and the corresponding required output \$V_{OUT}\$, to reveal \$V_{OFS}\$.

The trouble you have with that solution is finding a +2.475V source. If you have good, steady positive supply, you could use another op-amp for a low-impedance source (but it's not necessary, see below):

^{simulate this circuit}

A better solution would be to treat R1 and the 2.475V source as the Thevenin equivalent of some resistor divider between the 5V supply and ground. It's funny, we usually apply Thevenin's theorem to simplify resistor dividers into their Thevenin equivalent of a single voltage source and single resistor, but here we need to do the opposite!

Like the last schematic, you need resistors to derive 2.475V from a 5V supply, but their equivalent "paralleled" value should be 10k, to keep the gain correct at about 3. That is:

$$ \begin{aligned} 5 \times \frac{R_4}{R_3 + R_4} &= 2.475 \\ \\ \frac{R_3}{R_4} &= \frac{5}{2.475} - 1 \\ \\ R_3 &= 1.02 \times R_4 \\ \\ \end{aligned} $$

Paralleled they should be equivalent to 10kΩ

$$ \begin{aligned} \frac{R_3R_4}{R_3+R_4} &= 10k \\ \\ \frac{1.02R_4R_4}{1.02R_4 + R_4} &= 10k \\ \\ \frac{1.02R_4}{2.02} &= 10k \\ \\ R_4 &= 19.8k\Omega \\ \\ R_3 &= 1.02 \times R_4 \\ \\ &= 20.2k\Omega \\ \\ \end{aligned} $$

So, the simplest solution I can think of, assuming you have a stable 5V supply, is:

^{simulate this circuit}

Answer 2

You'll need a negative supply rail because the output swings to -5 V.