Phase shift oscillator: what is reducing loop gain and how does changing feedback resistor affect things?

Question

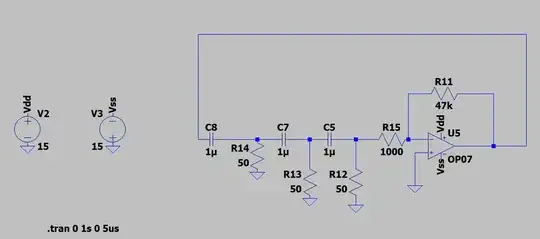
I have simulated the following circuit in LTSpice:

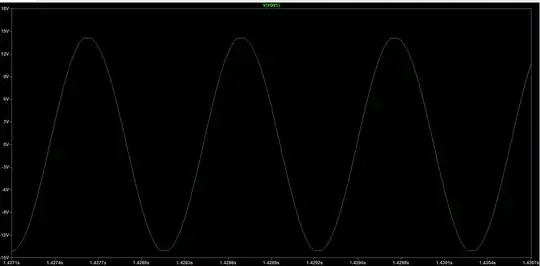
One can see that a stable sine wave with a peak of about 6.3 V is obtained, which has a frequency of 1 kHz (I calculated the RC network values to obtain 1kHz with the fromula which takes into account loading). There's very little distortion, too, in the sense that there's no clipping present. If I decrease the value of \$R_{11}\$ to about 35-36 k\$\Omega\$, then the frequency of oscillation will increase and its peak will further deacrease. If I increase the value of the same resistor, frequency will decrease and peak amplitude will increase. I tried to increase the value of the feedback resistor till 1.5 M\$\Omega\$, which halted oscillation, but I was never able to make the output saturate too much, which precisely means effectively obtaining a peak horizontal line instead of a point, similar to a square wave.

I was expecting to see some form of saturation, but it seems the op-amp continuously reduces loop gain until unity is reached during the short transient when oscillations are still increasing. Why is this happening? It seems there's no need for automatic gain control here.

I was thinking that maybe max op-amp output voltage swing falling with frequency is at play, but the corresponding graph in the OP07 datasheet did not convince me. How should I correlate the change of the feedback resistor value with its effects?

Thank you!

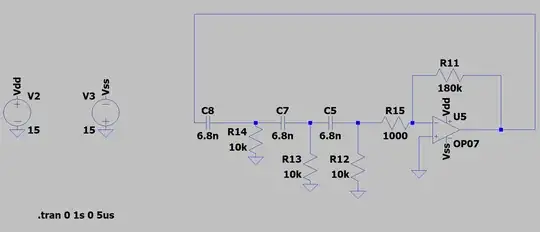
UPDATE 1: I re-calculated capacitor values to be able to use 10 k\$\Omega\$ resistors:

Now clipping is clearly present, as expected. Amplitude does not change with gain anymore, but frequency does. I am still trying to understand why current limiting didn't produce as much clipping before and I wonder why frequency still changes (might be useful for the others since @LvW says it is not covered in literature and I'm very curious about it, too)?

UPDATE 2:

I have eliminated \$R_{12}\$ and I have set \$R_{15}\$ to 10 k\$\Omega\$ so that the op-amp input resistor does not load change the bias of the last high-pass filter, as recommended by @Kevin White. It takes the oscillator a bit over a second to reach steady-state, which means just the right amount of op-amp gain is applied so as to make the oscillations start. The frequency of these oscillations is about 937 Hz.

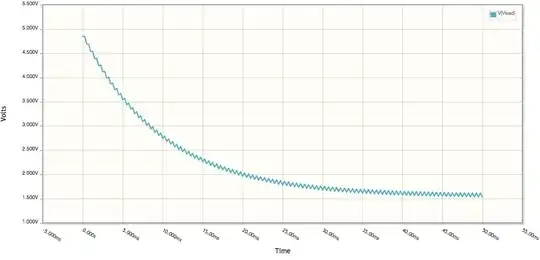
The only thing that keeps happening is that increasing \$R_{11}\$ still decreases frequency. I doubt the op-amp or the RC network are loaded this time. I have performed a simulation similar to that in @frr's answer (but with \$R_4\$ removed and with a resistor between V1 and ground before \$R_5\$ representing the feedback resistor) and varying the feedback resistor didn't change the filter response. I think the changing frequency has to do with how the waveform is distorted. Here is an example at how the waveform looks with the feedback resistor set to 400 k\$\Omega\$, obtaining a waveform of about 839 Hz:

So then, the last thing I am trying to figure out is how frequency still changes with gain.

Update 3:

Thanks everyone for your help! I have accepted one answer, however if I would have wanted to accept both that of @Kevin White and @James (but the site won't let me).

Answer 1

That high pass filter version of the phase shift oscillator has an inherent design flaw which causes a problem in a practical implementation of the circuit.

If we can firstly accept that saturation of the amplifier's output is a necessary requirement in the phase shift oscillator in order to stabilize the amplitude of the output waveform by using the saturation to reduce the loop gain to unity (one).

Although saturation is a necessary requirement, in the 3 high pass filter version of the phase shift oscillator, it is saturation which leads to a knock-on problem. During the period of time in each cycle when the amplifier's output waveform is saturated, and the input to the 3 high pass filters is held at a constant voltage, the 3 capacitors will be charging exponentially via their associated resistances. This puts a negative going spike into the sine wave at the output of the section of circuitry making up the 3 high pass filters.

So, at the output of the amplifier their is a non-linearity caused by saturation and at the output of the 3 high pass filter section their is a negative going spike occurring on the sine wave when it is at its negative peak.

To circumvent this inherent design flaw in the high pass filter version of the phase shift oscillator I would recommend using the low pass filter version instead ( 3 cascaded low pass RC filters). With this version, the 3 low pass filters work their magic to filter out most of the high frequency harmonics caused by the 'flat' on the waveform resulting from saturation. This leaves a nice low distortion sine wave at the output of the 3 low pass RC filters.

There is one small problem left to tackle, the output of the last RC low pass filter can be loaded by the amplifier's input resistor (particularly if this resistor has a relatively low value). To circumvent this problem, a unity gain buffer would be placed between the last RC low pass filter and the amplifier's input resistor.

The output sine wave would then be "tapped off" from the output of the unity gain buffer and amplified as necessary.

EDIT

I would suggest that there is a reduced oscillation frequency at the higher gain because at the higher gain there is more phase lag across the amplifier at any given frequency. When I say phase lag across the amplifier I mean closed loop phase lag.

The OPO7 has a GBW of 0.6 MHz and so with a closed loop gain of 30 (beta=1/31) the -3dB bandwidth will be 19.3 kHz. With a closed loop gain of 40 (beta=1/41) the -3dB bandwidth will be 14.6kHz.

The closed loop phase lag is -45 degrees at the -3dB frequency and so we can see that for the higher closed loop gain the phase lag must be higher at every frequency. The higher gain amplifier reaches the -3dB frequency, where the lag is -45 degrees, at a lower frequency.

In the ideal case where there is 60 degrees of lead across each RC section and 180 degrees of lag across the amplifier, the oscillation frequency will be:-

But in your situation there will be some extra lag across the amplifier giving a total closed loop phase lag for the amplifier of let's say -186 degrees at 955.5 Hz.

But the oscillator will stabilize at a slightly lower frequency where the loop phase lag is zero degrees. At this slightly lower frequency (937 Hz) the amplifier's closed loop phase lag might be (let's say) -183 degrees with 61 degrees of lead across each RC section. The increase of lead from 60 degrees to 61 degrees implies a reduction in frequency for a high pass filter.

Now if we increase the amplifier's closed loop gain further to 40, the amplifier's closed loop lag increases a bit more and the lead across each RC section also increases a bit forcing the frequency to reduce further (839 Hz).

So, I would say (until someone comes up with a better explanation) that the reduction in frequency that you are seeing is due to the amplifier's closed loop phase lag which increases as its closed loop gain is increased.

Suggestion

You could try an using op amp with a significantly higher GBW than that of the OP07 (0.6 MHz). This will have less closed loop phase lag at the gains and oscillation frequencies which you are dealing with. You could then see if the reductions in frequencies below the ideal frequency (955.5 Hz) are less than with the 0P07.

Answer 2

The 50 ohm resistors you are using in the phase-shift network are extremely low and are probably causing current-limiting in the output stage of the opamp.

The limiting will not happen at the peaks of the waveform where saturation would normally occur because of the phase shift in the RC network. With the approximately 60 degree phase shift of the first section I would expect saturation to occur about 60 degrees before the peak. The OP07 data sheet doesn't state maximum current but most opamps limit at 30-50mA. 50mA into the R14 (50 ohm) is about 5V pk-pk.

A more common value of the resistors would be between 10k and 100k with the capacitor value changed appropriately. Outside that range stray capacitance, leakage current or drive current can be problems.

For the final RC stage a preferred arrangement is to remove R12 and set R15 to 10k. As shown the final stage has a resistance value of 10k in parallel with 1k.

With R15 at 10k R11 would need to be about 300k to provide a gain of slightly more than 29, which is the attenuation of a 3-stage equal value RC network to provide 180 degrees of phase shift. If you need more gain than that something is not correct.

One common difficulty with simulating oscillators is how to get them to start-up. In real circuits noise or start-up transients provide the necessary stimulation. That may not exist in a simulation and an explicit start-up mechanism may need to be provided.

The OP07 amplifier is not very high gain bandwidth and the phase shift it incurs needs to be taken into account when calculating the oscillation frequency. Higher performance amplifiers will have less detrimental effect.

Answer 3

I've tried to approximately simulate, in QucsStudio, the amplitude and phase response of the third-order RC filter (high pass) in your feedback network.

Schematic:

And this is what I got:

Caveat: the step in the phase response may look way cool and dramatic - until you realize, that the phase domain is circular, 360 degrees total, and this is probably just the simulator's way of handling the smooth transition through +/- 180 degrees, between two consecutive horizontal "calculation points" in the simulation (I have no clue how to eliminate this step in the sim or in the display).

Then again, the point of 180 degrees is important. Because an ideal op-amp inverts the phase = shifts phase by exactly 180 degrees for the negative feedback network.

From the Nyquist's stability criterion, the circuit will want to oscillate at a frequency where total closed-loop amplification is greater than 1 (= gain greater than 0 dB) and the total phase shift is an integer multiple of 360 degrees. That's considering pure linear oscillation (no non-linear effects).

In my schematic, the source resistance (R5) is a substitute for the op-amp's output characteristics. As Kevin White has suggested, your original impedance of the RC filter could be "dangerously close" to the output impedance of your op-amp, which was likely affecting your results. By making the resistances in the filter way higher, you allowed the op-amp in your circuit to behave "closer to ideal". I have based my simulation of the latter version of your circuit, i.e. with 10k resistors to GND. I didn't really know what resistance to substitute for the op-amp, because on the one hand, op-amps have a limited current sourcing/sinking capability, but within that limit, the extreme open-loop gain makes the op-amp behave like a very low source impedance. So I just went with 200 Ohms to start with. When I decreased this to 2 Ohms, the resulting phase response has not changed very much. When I increased this to 10 kOhms, the tuning of the high-pass filter has shifted significantly lower, the 180deg phase transition was now at about 1 kHz. It's interesting BTW that your simulation puts this at about 1250 Hz = higher than my original result (about 1050 Hz).

I mean to say that increasing the effective output impedance (resistance) of the op-amp may lower the 180deg phase point of the RC filter and thus the oscillating frequency of the whole circuit.

Another factor is, that adding more gain may make your op-amp respond slower, i.e. add a wee bit more phase shift of its own. Thus, less phase shift needs to be contributed by the RC filter, less than 180 degrees. I'm wondering in which direction :-) I.e. another possible explanation of a frequency-shifting effect.

Yet another factor may be, that by cranking up the gain, you are worsening the non-linearity of the circuit. Close to the power rails, the gain gets lower, and during hard clipping, the AC amplification is effectively 0. I don't have a detailed picture in my mind, how this non-linearity would affect the overall frequency (with increasing gain) but intuitively, the clipping circuit behaves closer to a hysteretic multivibrator, where the frequency is partly determined by the slew rate at the edges and by the spacing of the up/down flipping threshold voltages. (And yes, by the RC delay.) This effect is especially strong in an RC sawtooth generator, using a proper comparator (or op-amp) as the hystheretic input. If you've ever built an astable multivibrator, just with logic gates or transistors, used a large elyt to filter its power, and disconnected the PSU and let the circuit "die slowly", you have probably observed some degree of a frequency-shifting effect as the power rail voltage was gradually sagging...

Even in your circuit, which appears neatly linear / sinusoidal, clipping in fact happens all the time, as long as the circuit oscillates. There needs to be a little bit of excess gain, for the oscillation to be self-sustaining. That excess gain gets wasted close to the power rails. If that excess is not too much, the clipping is "soft", hidden to the naked eye - it would appear in a spectral analysis as some content of higher harmonics, gradually growing as you would increase the gain.