More than 40 years ago I worked for a company that sold, modified, and serviced a wide range of electronic instruments, including wattmeters. In particular, we built watt transducers that used a core circuit comprised of just resistors, rectifiers, and transformers, based on a patent by Clarence W. Hewlett, Jr., and assigned to GE in 1972.
The transformers provided a voltage of about 6 VAC and a current of about 20 mA from external voltages of 120/240/480 VAC and current of 5 AAC for connection to larger CTs. The voltage typically varied only about 20%, but current could be anything up to the 5 A rating of the CT, and had an accuracy of about 1%.
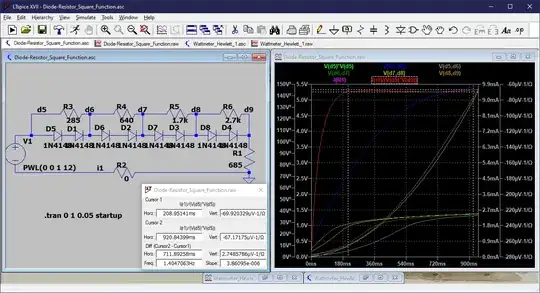
I think this is a valuable and useful circuit, especially as it does not require any separate power, and only very simple and basic components are required. I have made a simulation with resistor values that I basically selected by an educated guess, and perhaps a faded memory of when I worked on these transducers. I no longer have any of these transducers or detailed schematics showing the values.
The circuit works on the principle of a non-linear element using resistors in parallel with diodes, that perform a square function according to:
(E+I)^2 - (E-I)^2 = 4EI
Here are relevant images from the patent:
Here is my simulation:
And here are the output voltage values for various combinations of voltage and current. The second set of numbers are normalized based on the output and the V*I products for wattage. I think my values are pretty close, but I don't know quite how to calculate the best values.
I added additional diodes per the preferred configuration, and I plotted applied voltage vs current as well as V^2, and I/V^2, which ideally would be a constant for a perfect multiplier. I played around with resistor values until I got a pretty good curve fit. I have not yet incorporated this in the wattmeter simulation.
By using the slope of the V/I curve at various points, I was able to derive the resistance of the entire string of resistors (6000), and R6 (2700), although not very accurately once the diodes started conducting. So it looks like an empirical and experimental trial and error. But it looks like a logarithmic series is a close fit.
300, 600, 1200, 2400 versus 285, 640, 1700, 2700