In this:
I don't understand equation 3. How does 20·log10(...) - 94 dB = SPL?
If I did the example and solved the equation for 70 dB, I would get something around:
10(70+94)/20 · 6.3 · 10-3 = 998483 V
The result doesn't seem to make any sense and has nothing to do with the 0.399 VRMS stated.
How do I transform the Vout value computed from that equation to RMS?
Edit:
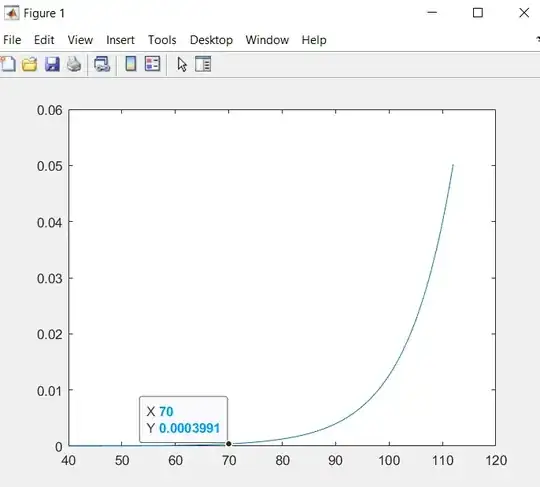
So using the things you guys told me I put the equation in MATLAB to do a sketch. This is what I got:
Very similar with the curve from the first image, what differs is the y axis. In the first image the y axis is in Vrms while the one i made in matlab is in V, if I multiply the y values with 1000 I seem to get the same result.
What is RMS in this context?