How does a capacitor-crystal-capacitor π-network produce a 180° phase shift in a Pierce Oscillator?

Question

The Pierce Oscillator consists of an inverting amplifier, a crystal in parallel with a biasing resistor as well as two capacitors connected between the legs of the crystal and ground, as in the following circuit, provided by Wikipedia.

As I understand it, when operated at series resonance, the crystal "looks" like a resistor, and as it's in parallel with R1 they can be combined into one resistor, so the circuit can be rewritten as follows (values chosen arbitrarily):

For the Barkhausen criteria to hold, the feedback network needs to phase shift the signal supplied by the output of U1 by 180°.

I don't really see how this is possible; to me R1//X1 should form a low-pass filter, which could at most phase shift the signal by 90°, and C2 should not affect the network at all as it's simply connected from the (assumed zero resistance) output of the amplifier directly to ground.

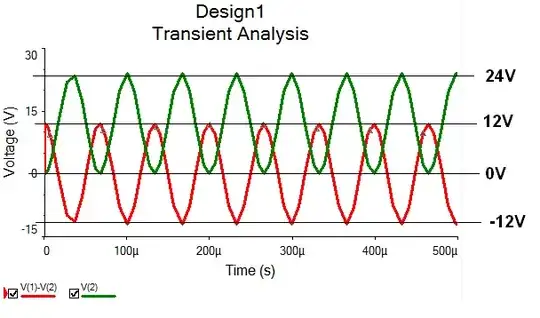
To test the workings of the network, I connected a signal generator to the input of the network and measured the output (using Falstad circuit simulator ), and got the following (small series resistances added to the capacitors as to avoid errors about resistance-free capacitor loops):

As one can see, the output of the feedback network (marked in red) is about 90° out of phase with the input signal (marked in green), as expected for a first order low-pass filter. Removing C2 does not make any noticeable difference to the operation of the circuit, matching my predictions.

So what does cause the extra 90° of phase shift in the feedback network? Am I missing some crucial component?

Answer 1

The Pierce circuit doesn't oscillate at the crystal's series resonance, but does oscillate at a slightly higher frequency, where its equivalent internal impedance is not resistive, but inductive.

When the crystal impedance is inductive, a 180 degree phase shift is possible:

^{simulate this circuit – Schematic created using CircuitLab}

In this example, crystal series resonance is \${1\over{2\pi\sqrt{L_1C_1}}}=4.594407 MHz\$
The network has a 180 degree phase shift at 4.5977585 MHz.

I've estimated that the CMOS gate's output impedance is 1500 ohms (a rough guess) because it is operating somewhat linearly. When used as a logic gate, output resistance is likely much smaller (below 100 ohms). At 100 ohms, the frequency where 180 degrees of phase shift occurs is 4.5989442 MHz.
In any case, the NMOS/PMOS inverter will likely not contribute exactly 180 degree phase shift to complete the Barkhausen requirement: loop phase of 0 degrees.

Manufacturers anticipate that their crystals will likely be used in oscillators of this type. Instead of specifying series resonant frequency in their data sheet, they specify that this is a "parallel-resonant" crystal, where their target frequency on the data sheet is stated along with a "load capacitance" of 8 picofarads.

Those two external 15pf capacitors are halved to 7.5pf, which would be close to the 8pf requirement. You might take the manufacturer's suggestion of 8pf as a hint that the usual one-or-two volts in these oscillator circuits won't cause excessive crystal current. Manufacturers don't want a bad rep for failed crystals, or wrong, drifty frequency.
Do try to make the series combination of C2 and C3 near the crystal manufacturers load capacitance. You're more likely to hit their target frequency, and keep crystal currents within bounds.