I'm reading AoE, there is a figure (p.26) for RC differentiator output and input voltages for step 5V input voltage with different slew rates (\$dV_{in}/dt\$). (It's time domain part. Only the rising edge of a step is shown.)
I understand the mathematics behind the chapter. So that \$V_{out} \approx RC\frac{dV_{in}}{dt}\$. But I'm trying to comprehend it in a physical sense, to carry out a mental experiment how electrons are "really flowing" inside the circuit and what's going on.
Many articles (when talking about step inputs) inspect the case when the input voltage is already 5V and a capacitor starts charging exponentially: \$V_{out} = V_f(1 - e^{-t/RC})\$.
But on the figure the input voltage is rising at a constant rate (e.g. \$dV_{in}/dt = 0.25V/ns\$). I imagine that at time zero the capacitor acts like a short circuit, so that all voltage "goes" to the resistor. Which "generates" \$I_R = I_C = I = \frac{V_{out}}{R}\$. This current charges the capacitor \$I = C\frac{dV_c}{dt}\$, so that voltage across the capacitor changes (increases).
At the beginning I believe that the input voltage change is greater than the capacitor voltage change (\$dV_{in} > dV_c\$), so that \$V_{out}\$ increases. At the same time as the output voltage increases, the current also should increase, which increases the capacitor rate of charge (\$dV_c/dt\$). The capacitor should be charging as \$x^2\$ (because the current is not constant). At some point in time the difference between \$dV_{in}\$ and \$dV_{c}\$ starts to decrease until it becomes zero. After that increase of \$V_{in}\$ equals to the increase of \$V_c\$ and \$V_{out}\$ stays const. (I could imagine it as pulling a spring at one end, the spring stretches and after while the other end of the spring jumps towards the first one)
I've found several answers on this topic but can't get the answer consistent with my thoughts:
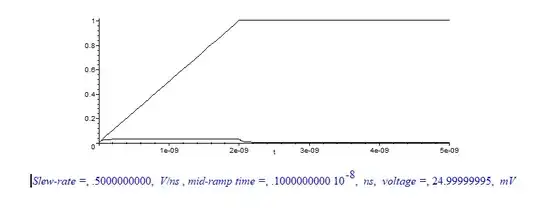
If we calculate the output voltage amplitude, we get: $$ RC = 50\Omega * 10^{-12}F = 50 * 10^{-3}ns = 0.05ns $$ $$ V_{out} = RC\frac{dV_{in}}{dt} = 50\Omega * 10^{-12}F * 0.25 * 10^9 V/s = 12.5mV $$
Which is consistent with the figure. But using the formula from the first answer and plotting a graph, it seems it gives a different answer. $$ V_{out}=V_{in}e^{-\frac{t}{RC}} $$ Where: $$ V_{in} = \frac{dV}{dt}*t $$
Powers of 10 are changed. But max value is different (4.6 vs 12.5) and the waveform is different.
According to the second answer we get that the current through the capacitor (if all the input voltage change was only across the capacitor) should be: $$ I = 10^{-12}F * 0.25 * 10^9 V/s = 250 \mu A $$
Which gives us (UPD 06.07.2022): $$ V_{out} = IR = 250 * 10^{-6}A * 50\Omega = 12500 * 10^{-6} V = 12.5 \mu V $$
At this level should be the voltage across the resistor (which is also the output voltage) to "generate" the current which charges the capacitor at the same rate as the input voltage increases. (P.S. The original post contained an error V=I/R, fixed this issue).
My questions are:
- What is the capacitor voltage waveform? (Is it S-like?)
- How to calculate the difference between \$dV_{in}\$ and \$dV_c\$ because of which \$V_{out}\$ increases?
- Why do the answers from the linked topics give different results?