To Start
Let's start with your diagram and work outward from it.
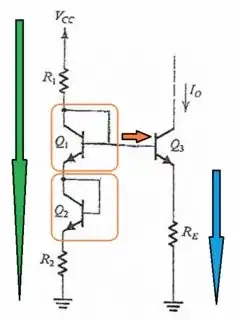
I'll add a few thoughts:
- Orange box around diode-connected \$Q_1\$. I'll call the voltage across it \$V_{_{\text{D}_1}}\$ to emphasize its diode-nature.
- Orange box around diode-connected \$Q_2\$. I'll call the voltage across it \$V_{_{\text{D}_2}}\$ to emphasize its diode-nature.
- \$I_{_{\text{R}_1}}\$: green-labeled current.
- \$I_{_{\text{R}_\text{E}}}\$: blue-labeled current.
- \$I_{_{\text{B}_3}}=0\:\text{A}\$: orange-labeled current. Obviously zero, since these are infinite \$\beta\$ BJTs.
Development
As \$I_{_{\text{R}_1}}\$ is the same current through \$Q_1\$ and \$Q_2\$ and \$R_2\$ (the green arrow), it follows therefore that \$V_{_{\text{D}}}=V_{_{\text{D}_1}}=V_{_{\text{D}_2}}\$ and \$I_{_{\text{R}_1}}=\frac{V_{_\text{CC}}-2\,V_{_{\text{D}}}}{R_1+R_2}\$.
Now, we know that the base voltage of \$Q_3\$ must be set by the base/collector voltage of \$Q_2\$, which is \$I_{_{\text{R}_1}}\,R_2+2\,V_{_{\text{D}}}\$. Therefore, it also follows that:
$$\begin{align*}
I_{_\text{O}}&=\frac{I_{_{\text{R}_1}}\,R_2+2\,V_{_{\text{D}}}-V_{_{\text{BE}_3}}}{R_{_{\text{E}}}}
\\\\
&= \frac{\frac{V_{_\text{CC}}-2\,V_{_{\text{D}}}}{R_1+R_2}\,R_2+2\,V_{_{\text{D}}}-V_{_{\text{BE}_3}}}{R_{_{\text{E}}}}
\\\\
&=\frac1{R_{_{\text{E}}}}\left[V_{_\text{CC}}\frac{R_2}{R_1+R_2}-2\,V_{_{\text{D}}}\frac{R_2}{R_1+R_2}+2\,V_{_{\text{D}}}-V_{_{\text{BE}_3}}\right]
\\\\
&=\frac1{R_{_{\text{E}}}}\left[V_{_\text{CC}}\frac{R_2}{R_1+R_2}+2\,V_{_{\text{D}}}\left(1-\frac{R_2}{R_1+R_2}\right)-V_{_{\text{BE}_3}}\right]
\end{align*}$$
Now, I've avoided a few details. The value of \$V_{_{\text{D}}}\$ is actually a function of its current and temperature. So it is really \${V_{_{\text{D}}}}_{\left(I_{_{\text{R}_1}},\,T\right)}\$. Similarly, since all the BJTs are identical, we can say that \$V_{_{\text{BE}_3}}={V_{_{\text{D}}}}_{\left(I_{_{\text{O}}},\,T\right)}\$.
So:
$$\begin{align*}
I_{_\text{O}}&=\frac1{R_{_{\text{E}}}}\left[V_{_\text{CC}}\frac{R_2}{R_1+R_2}+2\,{V_{_{\text{D}}}}_{\left(I_{_{\text{R}_1}},\,T\right)}\left(1-\frac{R_2}{R_1+R_2}\right)-{V_{_{\text{D}}}}_{\left(I_{_{\text{O}}},\,T\right)}\right]
\end{align*}$$
Sensitivity
The sensitivity equation comes from an easy to understand concept. You may want to know how much something changes when something else changes. But for engineering purposes, you really want to know how much something changes as a percent of its current value when something else changes by some percentage of its current value.
This is expressed mathematically as \$\frac{\%-\text{change}\: P}{\%-\text{change}\: Q}=\frac{\frac{\text{d}\, P}{P}}{\frac{\text{d}\, Q}{Q}}=\frac{\text{d}\, P}{\text{d}\, Q}\frac{Q}{P}\$.
If you know that, you can predict the sensitivity of your instrument. In this case, we'd like to know this: \$\frac{\%-\text{change}\: I_{_\text{O}}}{\%-\text{change}\: T}=\frac{\frac{\text{d}\, I_{_\text{O}}}{I_{_\text{O}}}}{\frac{\text{d}\, T}{T}}=\frac{\text{d}\, I_{_\text{O}}}{\text{d}\, T}\frac{T}{I_{_\text{O}}}\$.
For typical small signal BJTs, the variation of their BE junction voltage vs temperature is anywhere from \$-1.5\:\text{m}\frac{\text{V}}{\text{K}}\$ to \$-2.4\:\text{m}\frac{\text{V}}{\text{K}}\$ (this isn't constant over temperature for a specific device, by the way.) I honestly don't know if there is a standard symbol for this. But let's call it \$k_{_\text{be}}\$. This will have to be calibrated for any given BJT.
So, as an approximation we can say that \$\frac{\text{d}\,V_{_{\text{D}}}}{\text{d}\,T}=\frac{\text{d}\,{V_{_{\text{D}}}}_{\left(I_{_{\text{O}}},\,T\right)}}{\text{d}\,T}=\frac{\text{d}\,{V_{_{\text{D}}}}_{\left(I_{_{\text{R}_1}},\,T\right)}}{\text{d}\,T}\approx k_{_\text{be}}\$.
This allows us to say:
$$\begin{align*}
\frac{\text{d}\,I_{_\text{O}}}{\text{d}\,T}&\approx \frac1{R_{_{\text{E}}}}\left[k_{_\text{be}}\left(1-2\frac{R_2}{R_1+R_2}\right)\right]
\end{align*}$$
And if we set \$M=\frac{R_1}{R_2}\$, then the sensitivity expression is:
$$\begin{align*}
\approx k_{_\text{be}}\frac{T}{I_{_\text{O}}\,R_{_{\text{E}}}}\left[\frac{M-1}{M+1}\right]
\end{align*}$$
Worked Example
I just dumped in a model into LTspice and found that \$k_{_\text{be}}=1.75\:\text{m}\frac{\text{V}}{\text{K}}\$, examining temperatures going from \$300\:\text{K}\$ to \$303\:\text{k}\$, for a particular device I'd like to experiment with.
So, at \$300\:\text{K}\$ this works out to:
$$\begin{align*}
\approx \frac{525\:\text{mV}}{I_{_\text{O}}\,R_{_{\text{E}}}}\left[\frac{M-1}{M+1}\right]
\end{align*}$$
Let's assume that \$I_{_\text{O}}=I_{_{\text{R}_1}}\$ so that the base-emitter voltage differences are the same throughout the circuit. That's probably a helpful idea. And let's assume \$I_{_\text{O}}=1\:\text{mA}\$ and that the base-emitter voltage difference is then \$650\:\text{mV}\$. Finally, let's assume a sensitivity where the first factor (before applying \$M\$) is \$0.5\$, so that \$I_{_\text{O}}\,R_{_{\text{E}}}=1.05\:\text{V}\$ and therefore \$R_{_{\text{E}}}=1.05\:\text{k}\Omega\$. We can also then work out that \$R_2=400\:\Omega\$. (I won't worry, for now, about standard resistor values.)
With \$V_{_\text{CC}}=5\:\text{V}\$, I find that \$R_1=3.3\:\text{k}\Omega\$. This makes \$M\approx 8.25\$ and therefore the fully calculated sensitivity is now slightly less than \$0.5\$, or \$\approx 0.39\$. This means that I should expect to see, for a 1% change in temperature from \$300\:\text{K}\$ to \$303\:\text{K}\$, a change in current going from \$1\:\text{mA}\$ to \$1.0039\:\text{mA}\$. I'll use a collector resistor of \$2.2\:\text{k}\Omega\$. So I'd expect to see a change at the output of \$3.9\:\mu\text{A}\cdot 2.2\:\text{k}\Omega\approx 8.5\:\text{mV}\$.
Here's the LTspice schematic and output run:

The difference is about \$8.32\:\text{mV}\$, which is pretty close to prediction.
There's more to think about. But perhaps this gives a starting point?
I forget to check on the currents vs those used in designing the circuit. Let's look at the currents in the two legs, over temperature, versus the design line of \$1\:\text{mA}\$:
That also looks remarkably good. Keep in mind these are ideal BJTs. But, given that, things appear to work closely to what's expected. Also, note that the magenta curve shows that my estimate of \$650\:\text{mV}\$ is approached only at the higher temperature, \$303\:\text{K}\$, where the currents are exactly as designed. Had I designed for \$\approx 652.5\:\text{mV}\$, the currents would have crossed in the middle of the graph.